1 min to read
Adam Optimizer
Adaptive Moment Estimation Optimizer
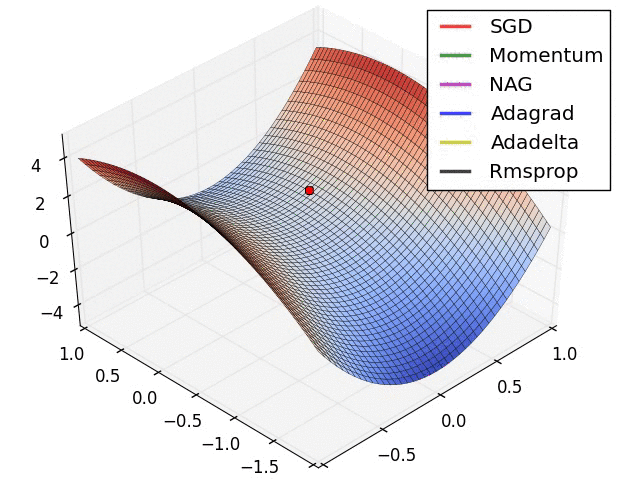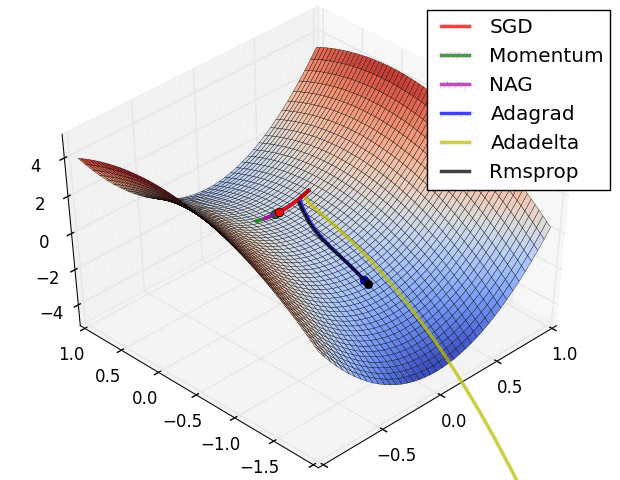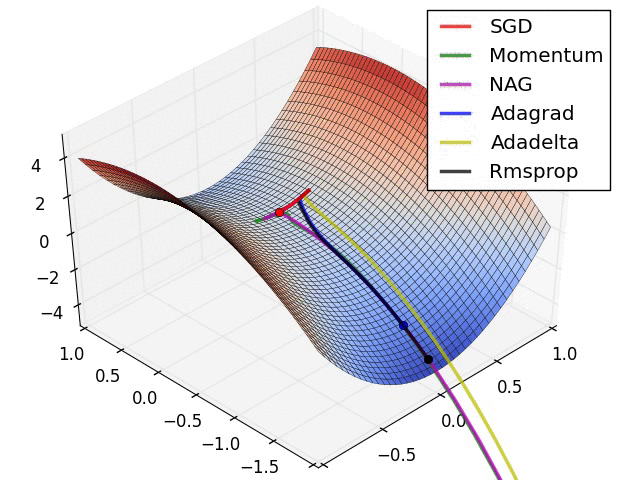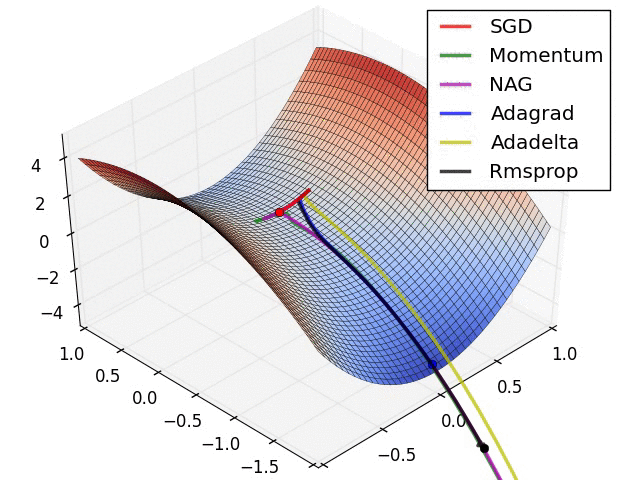
Adaptive Moment Estimation
Introduction
Adam(ADAptive Moment estimation)은 딥러닝에서 가장 널리 사용되는 최적화 알고리즘으로, Momentum의 안정적 방향성과 RMSProp의 adaptive learning rate를 결합한 방법론이다.
Adam은 gradient의 1st moment(평균)과 2nd moment(variance)를 추정하고, parameter마다 서로 다른 학습률로 곱해준다.
다른 최적화 알고리즘 (e.g., SGD, NAG, etc) 보다 빠르고 안정적이여서 딥러닝 모델에서 많이 쓰이고 있다.
Optimization
Deep Learning, Machine Learning 외 다양한 분야에도 최적화는 매우 중요하고 필수적인 요소이다.
그중 Deep Learning에서 최적화는 가중치를 loss function을 최소화 시키는 방향으로 업데이트하는 과정으로 학습하기 때문에, 최적화 함수와 손실함수가 성능과 output 등을 결정한다.
또한 일반적인 수학과 달리 비선형이고 non-convex이기 때문에 closed-form 해가 불가능하다.
Deep Learning에서 사용하는 최적화 함수는 GD(Gradient Descent), SGD(Strochasic Gradient Descent), RMSProp, 그리고 많이 사용하는 Adam(Adaptie moment estimation) 등 다양하게 존재한다.
Gradient Descent
경사하강법은 딥러닝 최적화에서 가장 중요한 존재이다.
함수의 기울기(gradient)가 내려가는 방향으로 parameter를 조금씩 이동시켜 손실 L을 최소화 시키는 방법이다.
경사하강법의 기본 공식은 다음과 같다.
\[\theta_{t+1} = \theta_{t} -\eta\nabla_{\theta}L(\theta_t)\]여기서 θ가 학습할 parameter이고, η는 step size, ∇L는 기울기이다.
기울기가 양수면 오른쪽, 음수면 왼쪽으로 내려간다.
이러한 경사하강법은 2가지의 문제점이 있다.
첫번째는 Step size이다. η(eta)는 우리가 설정하는 step size hyper parameter이고 이를 크게 잡으면 빠르게 수렴할 수 있지만 과도하게 설정하면 손실함수 최솟값 계산이 어려워지고 커지는 방향으로 최적화가 되버릴 수 있다.
두번째는 Local minima문제이다. 최적의 parameter를 위해 Gloval minimum을 찾아야 하지만, 경사하강법 특성상 parameter 시작점이 랜덤이기 때문에 Local minima에 빠져 수렴하게 된다.

Comments