2 min to read
Ensemble Learning, Bagging
Bootstrap AGGregatING
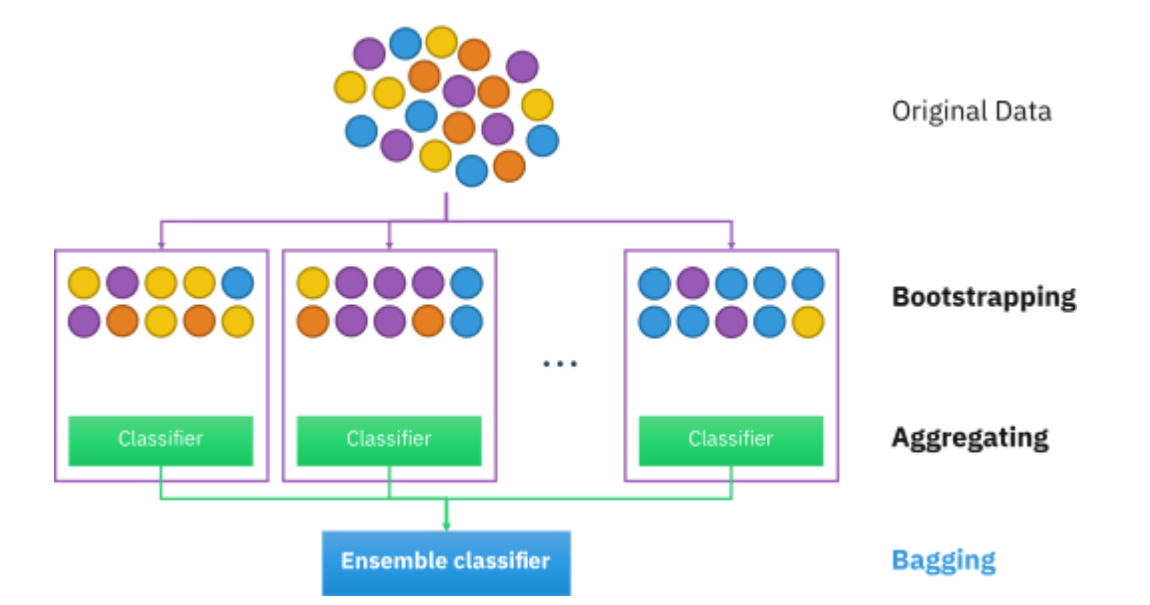
Ensemble Learning : Bagging
Abtract
Bagging (Bootstrap aggregating, 배깅)은 통계적 분류와 회귀 분석에서 사용되는 ML의 안정성과 정확도를 향상시키기 위해 고안된 Ensemble learning으로 variance(모델의 복잡성)를 줄이고 overfitting을 피하도록 해주는 알고리즘이다. 기존 학습 데이터로부터 랜덤하게 복원 추출하여 만들어진 새로운 데이터셋인 Bootstrap들을 기반으로 개별 모델을 학습하고 다시 결합함으로써 노이즈에 의한 변동성을 낮춰 안정성을 향상 시킨다.
Sampling with replacement
복원추출은 추첨후, 다음 추첨때도 중복이 가능하도록 뽑은 표본을 다시 모집단에 넣고 다른 표본을 추첨하는 방식이다.
예를들어 (1,2,3)에서 2개를 봅는것을 복원추출한다고 치면, 경우의 수가 9개가 된다. diversity에는 data에 대한 diversity와 model의 diversity가 있는데, Ensemble에서는 data의 diversity를 향상시킬때 복원추출을 사용한다.
Sampling without replacement
비복원추출은 추첨후, 한번 뽑힌 표본은 다시 뽑히지 않도록 다시 넣지않고 다른 표본을 추출하는 방법이다. 대표적으로는 k-fold data split이다. 전체 데이터를 k개의 부분집합으로 구분하고 하나의 부분집합에서 하나의 데이터만 뽑아서 validation을 수행하고 나머지는 training data로 쓰이는 대표적인 비복원 추출의 예시이다.
δ(.) : aggregation function
\[\hat y = \delta(f_1(x),f_2(x),...,f_k(x))\]하지만 k-fold data split은 전체 데이터를 사용하지 않고, k-1개의 데이터애 대해서만 학습하기 때문에 k개의 데이터가 손실된다는 점에서 많이 쓰이지 않고 있다.
Bootstrap Aggregating
Bagging은 bootstrap을 사용해서 여러 모델들에게 다른 데이터들을 학습시킨 후 평균내서 안정화시키는 Ensemble 기법이다. N개의 원본 데이터에서 N개를 복원추출하기 때문에 대략 63.2%의 데이터만이 포함되어 학습 데이터 끼리의 diversity가 생긴다.
\[P = (1-\frac{1}{N})^N \ \rightarrow \ \lim_{N \to \infty}(1-\frac{1}{N})^N = e^{-1} = 0.368\]Bagging은 low bias, high variance 인 모델에게 적합하다.
Low bias, High variance
bias가 적고 variance가 큰 상황은 평균적으로는 정답 근처까지 잘 맞추지만, 데이터가 조금만 바뀌어도 예측이 크게 변하는 상황이다. 대표적으로 깊은 Decision tree나 비정규화된 복잡한 모델이 그러한 예시이다.
Result Aggregating
Ensemble에서 결과를 aggregating하는 방법은 다양하다.
Majority voting
가장 많이 쓰이는 Majority voting이다.
\[\hat y_{Ensemble} = \arg \max_i (\sum_{j=1}^n \delta(\hat y_j = i), \ i \in \{0,1\})\]가장 단순하게 각 모델의 최종 클래스를 사용하여 안정적인 성능을 보인다. 대신 confidence에 대한 정보를 무시한다는 단점이 존재한다.
Weighted voting (Training accuracy)
다음은 각 모델의 출력에 weight (개별 모델들의 훈련 정확도)를 부여하는 방식이다.
\[\hat y_{Ensemble} = \arg \max_i (\frac{\sum_{j=1}^n(TrnAcc_j)·\delta(\hat y_j = 1)}{\sum_{j=1}^n(TrnAcc_j)}, \ i \in \{0,1\})\]보다 성능이 좋은 모델에 대해 가중치를 부여하여 더 좋은 성능을 낸다는 장점이 있지만, 튜닝을 해야한다는 단점이 존재한다.
Weighted voting (Predicted probability)
이번에는 각 confidence를 weight로 부여하는 방식이다.
\[\hat y_{Ensemble} = \arg \max_i (\frac{1}{n}\sum_{j=1}^n P(y=i), \ i \in \{0,1\})\]하지만 만약 모델이 overconfidence를 갖고있다면 크게 성능이 떨어질 수 있다는 단점이 있다.
Stacking
Stacking은 여러 base model들을 학습시키고, 각 모델의 출력을 새로운 feature로 사용해서 새로운 meta-learner를 생성해 최종 예측을 하는 방식이다.
Notation: g(·)
\[\hat y = g(f_1(x), f_2(x),...,f_M(x))\]Stacking은 모델간의 복잡한 상호작용까지 학습이 가능하며 성능 상한이 높지만, 구조가 복잡하고 과적합 위험이 크다는 단점이 있다.
Out Of Bag Error (OOB)
앞서 말했듯이, Bootstrap은 이론상 36.8% 정도가 누락되기 때문에, 해당 모델에게 그 샘플들은 보이지 않는 데이터 (Out of bag)이 된다. 따라서 누락된 데이터들만 모아서 Validation으로 사용한다.
Comments