5 min to read
Deep SVDD
about Deep SVDD
Deep SVDD
Introduction
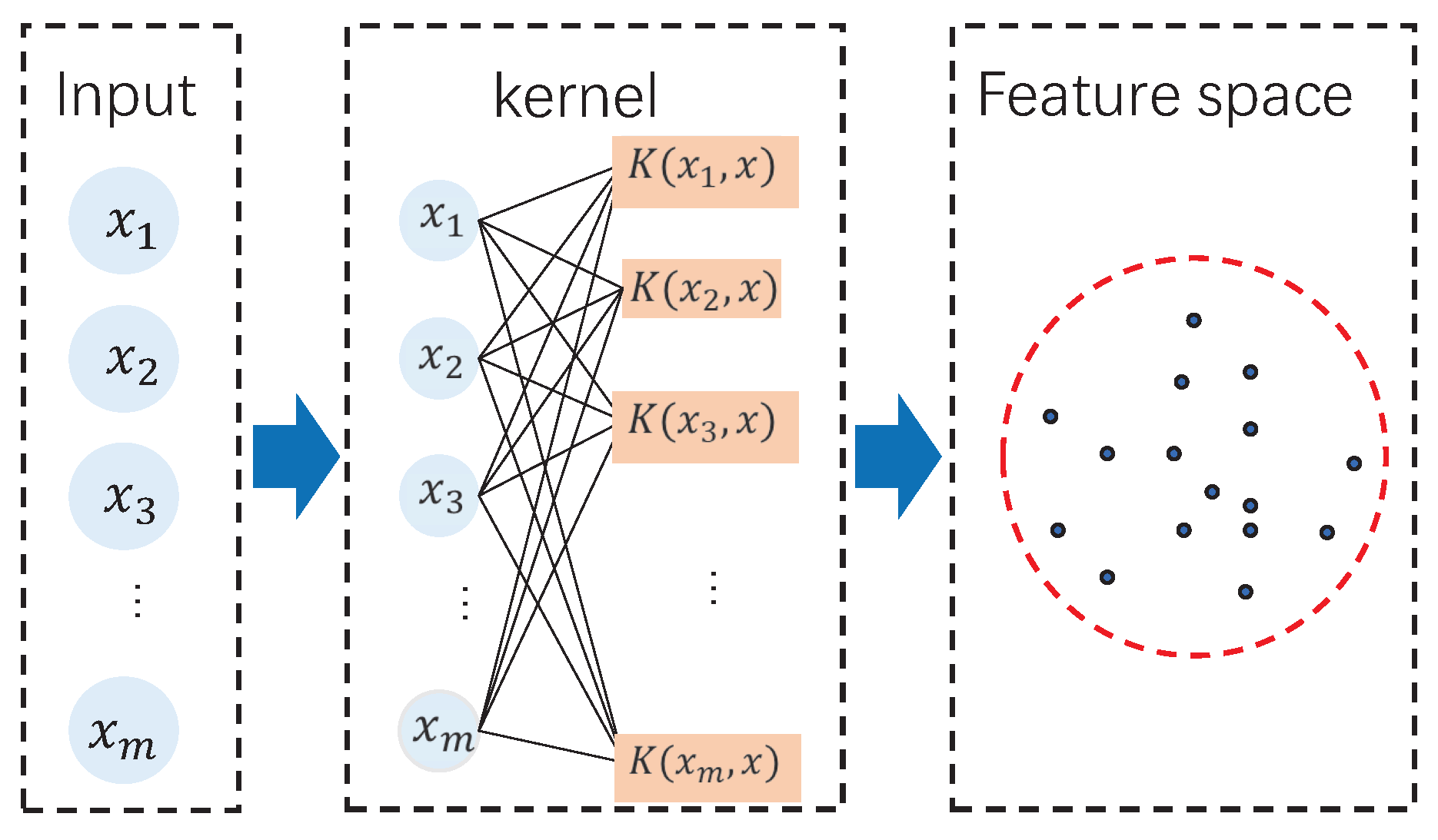
Support Vector 기반의 방법론들은 해석이 용이하고, Convex Optimization 문제로 정의되기 때문에 강한 이론적 기반을 갖고있다. 하지만 고차원 매핑을 위해 Kernel Trick을 사용함에도 불구하고, 고차원으로 갈수록 성능이 떨어지는 단점이 있다. (cf. 차원의 저주)
이를 해결하기위해 OCSVM은 Autoencoder와 결합하여 입력데이터를 latent space로 변환한뒤, on-class classification을 수행함으로써 성능을 극대화 시키고 있다.
Deep SVDD는 입력데이터를 저차원 latent space로 매핑한뒤, 하나의 중심으로 모이도록 학습하는 방식으로 모델링을 한다. 기존 SVDD는 고정된 feature space에서 최소 크기의 hypersphere을 학습하는 반면, Deep SVDD는 end-to-end 방식으로 하나의 통합된 프레임워크로 작동한다.
Deep SVDD
Deep SVDD는 기존 SVDD와 달리, 딥러닝 기반으로 한점 근처로 모으는 feature space를 학습하여 정상데이터를 둘러싸는 가장 작은 hypersphere를 찾고, 해당 경계를 기반으로 이상치를 탐지한다.
정상데이터는 구 내부로, 이상치는 구 외부로 보내는 가중치 W와 반지름 R을 학습한다.
SVDD objective function
\[\min_{c,R,\xi_i} R^2 + \frac{1}{\nu n}\sum_i\xi_i\]Notation
R : radius, c: center, ξ : slack variable, v : value for trade-off between ξ and volume
One-Class Deep SVDD (Unsupervised)
정상데이터만 있을 경우 모든 정상데이터를 한 구로 모으는 W를 학습하기 때문에 반지름 최소화없이 다음과 같이 정의한다
구의 최소화
다음과 같이 중심과 데이터의 거리를 정의할 수 있다
\[\|\phi(x_i;W)-c\|^2\]그리고 모든 데이터에 대한 거리를 최소화 시켜서 가장 작은 구를 만들기 위해 다음과 같이 정의한다
\[\min_W \frac{1}{n} \| \phi(x_i ; W) - c \| ^2\]가중치 정규화 (Weight decay)
\[\frac{\lambda}{2}\sum_l \|W^l\|^2_F\]가중치 W는 입력이 바뀌었을 때, 출력이 얼마나 크게 변하는 지를 나타낸다.
이러한 가중치의 크기에 대한 제약이 없을경우 overfitting과 출력 collapse로 이어질 수 있다.
따라서 Soft-boundary Deep SVDD의 목적함수는 다음과 같이 정의할 수 있다.
\[\min_W \frac{1}{n} \| \phi(x_i ; W) - c \| ^2 + \frac {\lambda}{2}\sum_l \| W^l \| ^2 _ F\]Soft-boundary Deep SVDD (Unsupervised)
대부분의 정상데이터를 최소 부피를 가진 구 안으로 mapping하는 R과 W를 학습한다
목적함수는 SVDD와 거의 비슷하다
반지름 최소화
정상 데이터는 안쪽으로
음수는 구 안을 의미하고 양수는 구 밖을 의미한다. 따라서 구 외부점에 대해서 계속해서 패널티를 주는 방식이다. 따라서 두번째 항은 다음과 같이 정의한다.
\[\frac{1}{\nu n}\sum_i\max(0, \|\phi(x_i;W)-c\|^2 - R^2)\]구 내부점은 0으로 되어 손실에 기여하지 않고, 구 외부점만 양수가 되어 손실에 기여한다
가중치 정규화 (Weight decay)
\[\frac{\lambda}{2}\sum_l \|W^l\|^2_F\]가중치 W는 입력이 바뀌었을 때, 출력이 얼마나 크게 변하는 지를 나타낸다.
이러한 가중치의 크기에 대한 제약이 없을경우 overfitting과 출력 collapse로 이어질 수 있다.
따라서 Soft-boundary Deep SVDD의 목적함수는 다음과 같이 정의할 수 있다.
Parameters
w : set of weights, R : radius
Hyperparameters
c : center, v ∈ (0,1] : value for proportion of outliers in a model, λ : value for controling the strength of weight decay regularization
\[\min_{R,W} R^2 + \frac{1}{\nu n}\sum_i\max(0, \|\phi(x_i;W)-c\|^2 - R^2) + \frac{\lambda}{2}\sum_l \|W^l\|^2_F\]Decision Function
학습된 구 경계면을 기반으로 정상데이터와 이상치 여부를 도출한다
정상데이터의 label을 -1, 이상치를 +1이라 두었을때 다음과 같이 정의할 수 있다
\[s(x) = \| \phi(x_i ; W) - c \|\] \[f(x) = sign(| \phi(x_i ; W) - c | ^2 - R^2 )\] \[y = \begin{cases} -1 & f(x) \geq 0 \\ +1 & f(x) < 0 \end{cases}\]구 내부 (정상데이터)
\[R > s(x) \rightarrow f(x) > 0\]구 경계 (Support vector)
\[R = s(x) \rightarrow f(x) = 0\]구 외부 (이상치)
\[R < s(x) \rightarrow f(x) < 0\]Optimization Deep SVDD
W는 representation learning이고 R은 만들어진 representation에 대한 radius이기 때문에 동시에 최적화하면 representation collepse가 발생될수도 있다
이를 방지하기 위해 k번째 epoch까지 W를 먼저 최적화를 한후, 학습된 W를 기반으로 R을 학습한다
Information-theoretic View
Unsupervised learning에서 input variable X를 latent variable Z로 압축하는 representation learning할때 압축률을 증가시켜야 한다.’
cf. autoencoder objective function
I(X;Z) : Z와 X의 dependancy를 증가 R(z) : downstream task
Information Theorem
정보량
사건 X가 발생하는 놀람의 정도를 반영하는 정보의 양
발생확률이 낮을수록 정보량이 커짐 (발생확률이 1일수록 0으로 수렴)
Entropy
발생가능한 모든 사건의 최소 평균 자원량
모든 사건의 결과가 비슷한 확률로 발생할때 불확실성이 커진다 (cf. Uniform distribution)
\[\mathcal H(X) = \mathbb E[I(X)] = \mathbb E[-\log p(x)] = -\int p(x)\log p(x)\]KL Divergence
두 확률 분포의 엔트로피 차이를 측정하는 지표
두 확률 분포에 대한 정보량으로 해석될 수 있으며, prior Q에서 posterior P로 이동할 때 얻어지는 정보량을 의미한다
(p에서 나온 데이터를 q로 설명할 때 필요한 평균 정보량)
Deep SVDD and Entropy Minimization
\[\mathcal H(z) = \mathbb{E}[-\log p(z)] = -\int{p(z)\log{p(z)}dz} \leq \frac{1}{2}\log((2\pi e)^d \det\Sigma)\] \[Z \sim N(\mu,\sigma^2,I)\]N(μ,σ^2,I) : Isotrophic Gaussian
\[\mathcal H(Z) = \frac{1}{2}\log((2\pi e)^d \det\sigma^2I) = \frac{1}{2}\log((2\pi e)^d(\sigma^2)^d) = \frac{d}{2}(1+\log(2\pi \sigma^2))\] \[\mathcal H(Z) \propto \log \sigma^2\]따라서 Deep SVDD objective는 구의 최소화에 대한 geometric term 뿐만 아닌 latent distribution의 entropy 최소화에 대한 probabilistic term으로도 해석가능하다
Deep SVDD objective function
\[\min_W \frac{1}{n} \| \phi(x_i ; W) - c \| ^2 + \frac {\lambda}{2}\sum_l \| W^l \| ^2 _ F\] \[\min_W \frac{1}{n}\sum_{i=1}^n \|f_W(x_i) - c\|^2\]Notation
f_W(x) : encoder
c : center
Deep SVDD and KL Divergence
만약 prior인 p(z)가 Isotrophic Gaussian이라면 Deep SVDD의 목적함수는 KL Divergence 최소화와 연결할 수 있다 \(p(z) = \mathcal N(c,\sigma^2, I)\)
\[-\log p(z) = \frac{1}{2\sigma^2}\|z-c\|^2 + C\] \[\mathbb E [\|f_W(x)-c\|^2] \iff E[-\log p(z)]\]p(z) : istrophic gaussian
\[KL(q_W(z) \| p(z)) = \mathbb E[\log q_W(z) - \log p(z)]\] \[= -\mathcal H(q_W(z)) - \mathbb E[\log p(z)]\] \[= -\mathcal H(q_W(z)) + \mathbb E[\frac{1}{2\sigma^2}\|z-c\|^2] + C\] \[\min_W KL(q_W(z)||p(z)) = \min_W \frac{1}{2\sigma^2} \mathbb E[\|z-c\|^2 -\mathcal H(q_W(z))]\]여기서 Deep SVDD는 구안으로 모으기 때문에 posterior q(z)또한 isotrophic Gaussian이라고 가정하면
\[q_W(z) \sim \mathcal N(\phi,\sigma^2,I)\] \[\mathcal H(q_W(z)) = \frac{d}{2}\log(2\pi e \sigma^2)\]뒤와 같이 Entropy가 어떠한 상수가 되기 때문에 KL Divergence식이 L2 Norm으로 되어 One-Class Deep SVDD의 목적함수는 KL Divergence minimization으로도 표현할 수 있다
\[\min_W KL(q_W(z)∥p(z)) = \min_W \mathbb E\|z-c\|^2\]Reference
[1] L. Ruff, R. A. Vandermeulen, N. Görnitz, L. Deecke, S. A. Siddiqui, A. Binder, E. Müller, and M. Kloft,
“Deep One-Class Classification,”
in Proc. 35th Int. Conf. Mach. Learn. (ICML), Stockholm, Sweden, 2018,
[2] L. Ruff, J. R. Kauffmann, R. A. Vandermeulen, G. Montavon, W. Samek, M. Kloft, and K.-R. Müller,
“Deep Semi-Supervised Anomaly Detection,”
in Proc. 8th Int. Conf. Learn. Represent. (ICLR), Addis Ababa, Ethiopia, 2020.
[3] paper review: Deep SAD

Comments