January 20, 2026 5 min to read

Ensemble Learning

Ensemble Overview

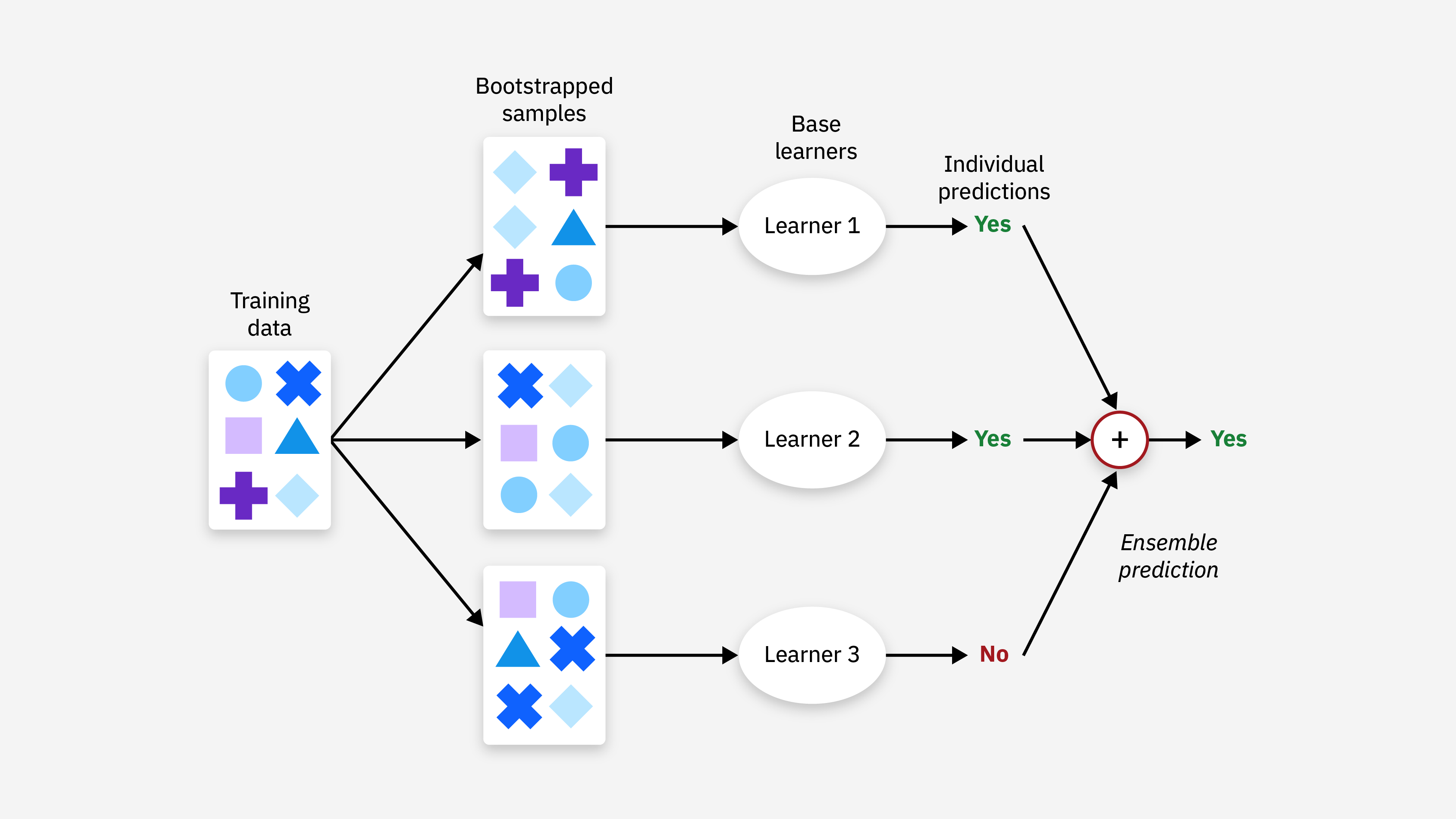
Ensemble Learning Methods

Abstract

Ensemble(앙상블) 기법은 하나의 강력한 성능을 보이는 모델을 만드는 대신, 여러개의 상대적으로 단순한 모델들을 결합하여 성능과 안정성을 향상 시키는 모델이다. Ensemble 기법의 가장 큰 장점은 서로 다른 모델의 예측을 결합하기때문에 단일모델보다 예측성능을 향상 시킬 수 있으며, 과적합 완화를 시킬 수 있다. 하지만 여러 모델을 사용해야 하기 때문에 계산 비용이 증가하고 해석 가능성이 감소될 수 있다. 이러한 Ensemble 기법의 장점과 특징들을 알아보자.

No Free Lunch Theorem

“No Free Lunch Theorem”은 1997년에 발표된 논문인 “No Free Lunch Teorems for Optimization” 에서 나왔으며, 특정한 task에 최적화 되어있는 모델은 당연히 다른 문제에서는 타 모델에 밀리는 것은 당연하고 이는 곧, 항상 우월하거나 열등한 모델은 존재하지 않는 것을 의미한다. 좋은 일반화 성능을 이끌어내는 것이 목표라면, context-independent나 usage-independent 와 관계없이 어느 한쪽만을 선호할 이유는 없다.

Ensemble Learning Method

ML과 DL에서 Ensemble은 학습 알고리즘들을 따로 쓰는 경우에 비해 더 좋은 예측 성능을 위해 다수의 학습 알고리즘을 사용하는 방법이다. 이는 여러 모델의 예측을 결합해서 더 정확한 결정을 내리고 복잡한 문제들도 여러개의 하위 문제로 나누어 효율적으로 해결할 수 있다.

Empirical Evidence

2014년에 발표된 논문 179개의 알고리즘과 121개의 데이터셋을 사용한 “Do we Need Hundreds of Classifiers to Solve Real World Classification Problems?” 에 따르면 Rank 1인 알고리즘은 존재하지 않았으나 (i.e. no free lunch theorem), 각 알고리즘의 상대적인 순위는 통계적으로 유의미한 수준이고 Random Forests와 SVM 계열이 상대적으로 분류성능에 대해 높게 측정되었다.

Bias-Variance Decomposition

Additive Error Model

Additive Error Model은 현실 세계의 데이터에는 데이터를 생성하는 정답 매커니즘이 있더라도, 노이즈가 항상 존재한다는 가정이다.

\[y = f(x) + \epsilon, \quad \epsilon \sim \mathcal N(0,\sigma^2)\]

f(x)는 우리가 학습시키려는 목표 함수지만, 실제로는 알 수 없다.

또한 전체 데이터에서는 우리가 원하는 값을 얻을 수 있지만, 포인트 하나하나에 대해서는 분포형태를 띈다. 여러 모델들을 노이즈로 인해 생성된 많은 데이터 셋으로 학습시켰을 때의 평균 함수는 다음과 같다.

\[\bar F(x) = \mathbb E[\hat F_D(x)]\]

Bias-Variance Decomposition

Bias-Variance Decomposition을 보여주는 가장 대표적인 예시는 MSE(Mean Squared Error)를 가지고 유도하는 것이다. MSE는 target과 prediction의 오차를 제곱한 후에 기댓값을 취하는 것이다.

노이즈의 분산 분해

\[MSE = \mathbb E[(y-\hat f(x))^2]\] \[= \mathbb E[(f(x)+\epsilon-\hat f(x))^2]\] \[=\mathbb E[(f(x)-\hat f(x))^2 + \epsilon^2 +2(f(x)-\hat f(x))\epsilon]\] \[=\mathbb E[(f(x)-\hat f(x))^2] +\mathbb E[\epsilon^2] + 2\mathbb E[f(x)-\hat f(x)]*\mathbb E[\epsilon]\]

이때 노이즈는 평균 0, 분산이 유한한 분포를 따른다고 가정하기 때문에 3번째 term이 사라진다.

또한 다음의 분산 식에 따라

\[Var(X) = \mathbb E[X^2] - \mathbb E[X]^2\] \[\mathbb E[\epsilon^2] = Var(\epsilon) + \mathbb E[\epsilon]^2\]

여기서 평균이 0이기때문에 2번때 term은 분산이 된다.

\[\therefore \mathbb E[(f(x)-\hat f(x))^2] + \sigma^2\]

bias의 분산 분해

다음은 bias의 제곱과 분산으로 분해 유도 과정이다.

\[\mathbb E[(f(x)-\hat f(x))^2] = \mathbb E[(f(x)-\bar f(x) + \bar f(x) - \hat f(x))^2]\] \[= \mathbb E[(f(x)-\bar f(x))^2 + (\bar f(x) - \hat f(x))^2 + 2(f(x)-\bar f(x))(\hat f(x) - \bar f(x))]\] \[= \mathbb E[(f(x) - \bar f(x))^2] - \mathbb E[(\hat f(x) - \bar f(x))^2] + 2\mathbb E[f(x) - \bar f(x)]* \mathbb E[\hat f(x) - \bar f(x) ]\]

이때 3번째 term은 다음과 같기 때문에 0으로 사라진다.

\[\mathbb E[\hat f(x)] - \mathbb E[\mathbb E[\hat f(x)]] = 0\] \[\therefore \mathbb E[(f(x) - \bar f(x))^2] - \mathbb E[(\hat f(x) - \bar f(x))^2]\]

위 분해는 모델과 무관하게 데이터 생성과정에서 노이즈가 있으면 완벽한 모델도 오차 0은 불가능함을 시사한다. Bias는 실제 정답과의 차이를 보여주고, 분산은 평균으로 부터 퍼짐 정도를 나타낸다.

Bias-Variance Dilemma

Bias와 분산을 둘다 낮출수 있다면 좋겠지만, 단일 모델로는 둘다 줄이기는 쉽지 않다. bias를 낮추면 그만큼 variance가 높아지기 때문이다.

Bias가 낮고 variance가 클때 variance를 줄이는 목적으로 사용하는 기법이 bagging기법이다 .

반면에, Bias가 높지만, variance가 낮을때 둘다 낮추는 기법이 boosting 계열이다.

정리하면 어떤 상황이든 여러 계열의 기법을 사용할 수 있지만, bias가 낮고 variance가 큰, 즉, 모델의 복잡도가 높을때 bagging과 잘 맞고, high bias low variance일때 즉, 모델의 복잡도가 낮을때는 boosting이 잘 맞는다.

Purpose of Ensemble

본론으로 돌아와, Ensemble의 목적은 여러개의 학습 모델을 결합하여 error를 낮추는 것이다.

앞서 말했듯이, variance를 줄이기 위해서는 bagging, random forest 기법들이, bias를 줄이기 위해서는 Adaboost 기법 등이 사용된다. 이때, Ensemble기법으로 좋은 성능을 내기 위해서는 여러 모델들이 같은 실수를 반복하지 않도록, 다시말해 충분한 다양성(sufficient degree of diversity)가 필요하다.

너무 동일한 모델들 (a set of identical models)만을 결합하면 효과를 못보기 때문에, 일정 수준 이상의 다양성은 유지하면서, 개별적인 모델들도 좋은 성능을 가져야 한다.

Diversity: Implicit (Independent) vs Explicit (Model guided)

먼저 Implicit Diversity는 diversity를 직접 측정하거나 강제하지않지만, 다른 랜덤한 학습 데이터를 각각의 모델에게 제공하면서 다양성을 준다.

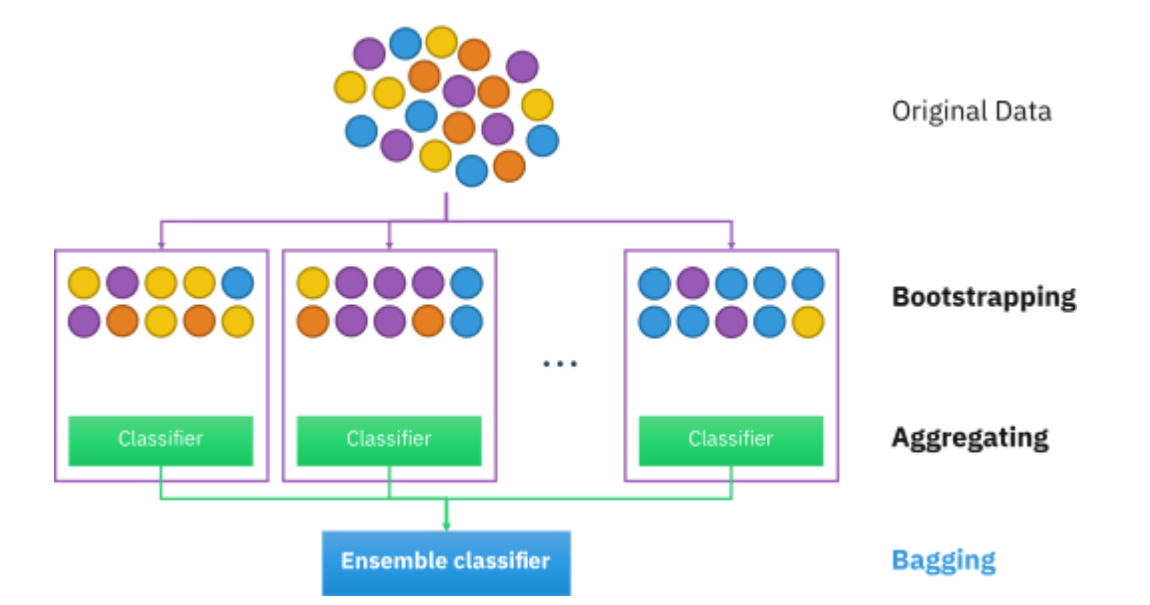
대표적으로 데이터 샘플 (Instance)를 바꾸면서 학습하는 bagging, variable를 바꾸는 Rotation Forest, 둘다 바꾸면서하는 Random Forest 등이 있다.

Explicit Diversity는 다양성을 목표로 삼아 직접 제어한다. 손실함수에 직접적으로 penalty를 부여함으로써 diversity를 강제한다. 대표적으로 Boosting이 있다.

Independent istance selection (Implicit)은 데이터가 모델을 보지않고 나뉘기 때문에, 병렬적으로 처리가 가능한 반면, Model guided selection (Explicit)은 모델의 상태에 따라 나뉘기 때문에 순차적으로 진행된다.

Why Ensemble

결론적으로는 Ensemble은 여러 모델의 오차를 평균내기 때문에, 오차들이 서로 independent(or uncorrelated) 할때 variance가 줄어들기 때문에 성능이 향상된다.

다음과 같이 모델을 함수와 오차로 분해할때,

\[y_m(x) = f(x) + \epsilon_m(x)\]

각 모델은 함수 주변에서 각 오차만큼 다르게 흔들린다.

이때 각 모델의 MSE는 자기 오차의 분산임을 알 수 있다.

\[\mathbb E_x[(y_m(x)-f(x))^2] = \mathbb E_x[\epsilon_m(x)^2]\]

따라서 각 모델들의 평균 오차는 다음과 같은 반면,

\[E_{avg} = \frac{1}{M}\sum_{m=1}^M\mathbb E_x[\epsilon_m(x)^2]\]

Ensemble의 출력을 개별 모형의 출력의 평균으로 정의했을때, Ensemble의 기대 오차는 다음과 같다.

\[E_{Ensemble} = \mathbb E_x[(\frac{1}{M}\sum_{m=1}^M y_m(x) - f(x))^2]\] \[= \mathbb E_x [(\frac{1}{M}\sum_{m=1}^M \epsilon_m(x))^2]\]

따라서 오차의 평균이 0이고, uncorrelated하다면, 오차가 M배만큼 줄어든다.

하지만 현실에서 오차의 상관관계가 존재하더라도, Cauchy’s inequality에 의해 오차가 하한이 되어 적어도, single best 모델보다는 낫다는 것을 보여준다.

\[[\sum_{m=1}^M \epsilon_m(x)]^2 \leq M\sum_{m=1}^M \epsilon_m(x)^2 \rightarrow [\frac{1}{M}\sum_{m=1}^M \epsilon_m(x)]^2 \leq \frac{1}{M}\sum_{m=1}^M\epsilon_M(x)^2\] \[\therefore E_{Ensemble} \leq E_{Avg}\]