6 min to read
One-Class Support Vector Machine
OCSVM
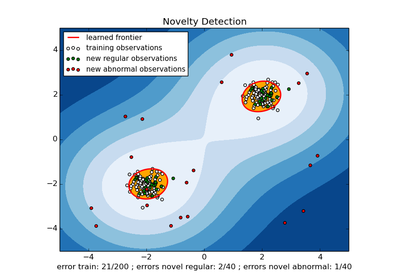
One-Class SVM
Introduction
One-Class Support Vector Machine (OCSVM) 은 정상 데이터만을 이용해 정상 데이터가 분포하는 영역을 최대한 작게 포괄하는 결정 경계 (hypersphere or hyperplnae) 을 학습함으로써, 그 바깥에 위치하는 관측치를 이상치로 간주하는 알고리즘이다.
정상 데이터만을 이용해 결정함수를 학습하는 semi-supervised model이며, 주어진 데이터의 대부분이 포함되는 최소 영역을 찾는다.
그리고 정상데이터 영역 밖의 새로운 형태의 데이터는 novelty로 간주하여 novelty detection 알고리즘이다.
RBF, polynomail, signoid 등의 Kernel trick을 적용함으로써 비선형 구조를 갖는 데이터에도 결정 경계 학습이 가능하며, 특히 고차원 또는 복잡한 manifold 구조의 정상 데이터를 효율적으로 감싸기 때문에 다양한 도메인에서 널리 활용 된다.
Support Vector-based Novelty Detection
SVM 원리를 이용해 이상치 탐지하는 기법이 널리 사용되고있다.
label이 정상데이터만 있을때 그 데이터에 대한 boundary를 학습하고 그 boundary 밖에 데이터를 이상치로 판단하는 방법이다.
대표적으로 OCSVM과 SVDD가 존재한다.
One-Class Support Vector Machine
SVM이 두 support vector 간의 margin을 최대화 시켰다면 OVSVM 은 정상데이터와 원점과의 간격을 최대화시킨다.
과정은 SVM과 비슷하다. SVM에서 margin의 최대화, 올바른 분류(부등식 제약)으로 정의되었다면, OCSVM은 크게 4가지로 본다.
정상 데이터는 경계 안쪽으로
경계의 형태(초평면)는 다음과 같은 형태일 것이다.
\[w^{T}\phi(x) = \rho\]여기서 차이점은 x가 아닌 ϕ(x)를 쓴다는 점인데, 똑같은 x이고 SVM의 특성 상 고차원일수록 경계가 복잡해져 저차원 feature space로 보내는 mapping function이다.
보통 Kerner Trick을 사용해서 실 계산은 잘 하지 않는다.
그리고 정상데이터는 안쪽으로, novelty 데이터는 바깥쪽이므로 다음과 같이 쓸 수 있다.
\[w^{T}\phi(x) ≥\rho\]그리고 Soft-Margin SVM가 마찬가지로 제약을 완화시켜주는 slack변수 까지 두면 첫번째 목적식이 나온다.
\[w^{T}\phi(x_i) \ge \rho - \xi_i,\qquad \xi_i \ge 0\]변동성 최소화
hyperplane에서 w(gradient, 기울기)는 변동성을 의미한다.
훈련 데이터의 변동에 따라 모델 출력의 변동 비율인데, 일반적인 함수의 기울기에 대한 정의를 생각하면 편하다.
하지만 w가 크다는 것은 곧 변동성이 크다는 것을 의미하고, 이는 훈련데이터가 조금만 변해도 모델 출력이 크게 바뀌게 되어, 특정 패턴에 과도하게 반응하거나, training set에 과적합, noise에 따라가는 등, 불안정하게 된다.
따라서 변동성 최소화 즉, w크기를 최소화를 시킨다.
\[\min_{w} \ \frac{1}{2}\|w\|^{2}\]앞에 1/2상수는 SVM과 동일하게 Lagrange + KKT를 통해 opimization을 하는데 미분과정에서 2가 곱해져서 단순한 꼴을 위해 추가한 것이고 상수가 추가되었다고 값이 변하지는 않는다.
정상데이터 영역을 원점에서 최대한 멀리 보내야한다
위 그림에서 보이다싶이, 원점과 정상데이터의 거리는 ρ로 표시한다.
앞에서 언급했듯이, 일반화 성능과 더 좋은 성능을 위해 정상데이터를 원점에서 멀리 보내야 한다.
따라서 다음과 같은 목적함수를 얻을수있다.
\[\min -\rho\]약간의 오분류 허용
Soft-Margin SVM랑 똑같이 slack 변수 ξ(xi)를 추가함으로써 약간의 오분류를 허용한다.
위에서 조절하는 파라미터가 C 였다면 OCSVM에서는 ν(nu)를 통해 조절할 수 있다.
이 ν가 OCSVM에서 핵심적인 역할을 하기때문에 ν-SVM이라고 부르는 경우도 존재한다.
각 데이터에 대한 개별 slack의 합을 다음과 같이 표현할 수 있다
\[\sum{\xi_{i}}\]이때 xi는 경계 안 또는 경계 위 (정상범위 안)에서는 0이고, 오분류일때는 0보다 크기때문에 slack의 크기는 곧 얼마나 오분류를 했는지는 나타낸다.
그리고 이를 평균을 내면 오분류의 비율을 알 수 있다.
\[\frac{1}{n}\sum{\xi_{i}}\]여기에 우리가 정할 수 있는 parameter nu를 붙임으로써 이 비율을 조절할 수 있다.
\[\frac{1}{\nu n}\sum\xi_{i}\]nu를 분수에 넣음으로써 nu가 크면 slack panelty가 작아지고, 작으면 커지기때문에 nu가 클수록 outlier를 더 많이 허용한다.
위 과정을 다 합치면 다음과 같은 최적화함수를 얻을 수 있다.
\[\min_{w,\,\rho,\,\xi} \; \frac{1}{2}\|w\|^{2} - \rho + \frac{1}{\nu n}\sum_{i=1}^{n} \xi_i\] \[\text{s.t.} \qquad w^{T}\phi(x_i) \ge \rho - \xi_i, \qquad \xi_i \ge 0.\]Optimization
SVM과 마찬가지로 Lagrange + KKT조건을 사용해서 최적화 시킨다.
제약조건이 2개이기 때문에 다음과 같이 2개로 나눈다.
그러면 우리가 구해야하는 L함수를 다음과 같이 쓸 수 있다.
\[L(w, \rho, \xi; \alpha, \eta) = \frac{1}{2}\|w\|^2 - \rho + \frac{1}{\nu n}\sum_{i=1}^n \xi_i - \sum_{i=1}^n \alpha_i \left( w^\top \phi(x_i) - \rho + \xi_i \right) - \sum_{i=1}^n \eta_i \xi_i\]첫번째 Stationary로 각각 편미분을 해준다.
\[\text{(1) } w \text{ 에 대해} \\ \frac{\partial L}{\partial w} = w - \sum_{i=1}^{n} \alpha_i \phi(x_i) = 0 \Rightarrow w = \sum_{i=1}^{n} \alpha_i \phi(x_i)\] \[\text{(2) } \rho \text{ 에 대해} \\ \frac{\partial L}{\partial \rho} = -1 + \sum_{i=1}^{n} \alpha_i = 0 \Rightarrow \sum_{i=1}^{n} \alpha_i = 1\] \[\text{(3) } \xi_i \text{ 에 대해} \\ \frac{\partial L}{\partial \xi_i} = \frac{1}{\nu n} - \alpha_i - \eta_i = 0 \Rightarrow \alpha_i + \eta_i = \frac{1}{\nu n}\] \[\text{여기서 } \alpha_i \ge 0,\ \eta_i \ge 0 \text{ 이므로} \\ 0 \le \alpha_i \le \frac{1}{\nu n}\]위에서 구한 조건들을 각각 L함수에 넣으면 α에 대한 dual function으로 만들 수 있다.
\[\sum_{i=1}^{n} \alpha_i = 1,\quad \alpha_i + \eta_i = \frac{1}{\nu n}\]위를 대입하면 rho와 xi는 없어져서 다음과 같이 쓸 수 있다.
\[L = \frac{1}{2}\|w\|^{2} - \sum_{i=1}^{n} \alpha_i\, w^{T}\phi(x_i).\]그리고 w에 대한 alpha식
\[w = \sum_{i=1}^{n} \alpha_i \phi(x_i)\]을 대입하고 정리를 하면 다음 함수를 얻을 수 있다.
\[L(\alpha) = \frac{1}{2} \sum_{i,j} \alpha_i \alpha_j k(x_i, x_j) - \sum_{i} \alpha_i \sum_{j} \alpha_j k(x_j, x_i).\]이를 합치고 잘 정리하면 최종함수를 다음과 같이 쓸 수 있다.
\[\min_{\alpha} \; \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j k(x_i, x_j)\] \[\text{s.t.} \quad \sum_{i=1}^{n} \alpha_i = 1, \qquad 0 \le \alpha_i \le \frac{1}{\nu n}, \quad i = 1,\dots,n.\]그리고 decision function은 w의 alpha에 대한 식을 원래 hyperplane식에 대입함으로서 구할 수 있다.
\[f(x) = \sum_{i=1}^{n} \alpha_i\, k(x_i, x) - \rho\]Location of a point
이제 각 조건에 대해 데이터 위치를 알 수 있다.
Case 1 같은 경우에는 SVM과 동일하다.
Case 2,3 같은 경우에는 alpha가 양수이기때문에 Support Vector 후보군이된다.
여기서 Case 3같은 경우에는 우리가 구했던 다음조건에 대입하면
\[\alpha_i + \eta_i = \frac{1}{\nu n}\]다른 라그랑즈 상수가 0이 나오게 되고, 이는 곧 slack변수가 양수가 되어 outlier 후보군이 된다.
Case 2 경우를 대입하면 0이 안나오고 곧, slack이 0이되어 hyperplane 내부의 support vector가 나온다.
ν의 의미
alpha의 최대값은 항상 다음과 같다
\[\alpha_{i}^{max} = \frac{1}{\nu n}\]예를들어 sample개수가 1000개고, ν = 0.1이면 0.01이 나올것이다. 즉, outlier가 된 훈련데이터라면 alpha_i는 0.01이 되는것이다.
우리가 구한 조건중 모든 alpha의 합은 1이여야 한다는 것이 존재했다.
이는 곧, v가 0.1일때 alpha가 0.01이기 때문에 이러한 점이 100개가 존재해야 1이 될 것이고, alpha가 양수일때만 support vector이기때문에 support vector 100개에 아닌점 900개 로 해석할 수 있다.
이를 정리하면 다음 식에 따라 support vector는 최소 vn개 가져야 한다.
\[\frac{1}{\nu n} \cdot \nu n = 1\]또한 alpha가 1/200이고, support vector 개수가 200이면, 1/vn인 alpha가 존재하지 않을 것이고, 따라서 xi가 다 양수인점이 존재하지 않아 경계 바깥의 점이 없을것이다.
따라서 vn의 의미는 경계밖에 존재하는 support vector의 최대개수를 의미한다.
이를 다시 생각해보면 v의 값에 따라 경계 밖에 존재하는 support vector 최대 개수와 내부 개수의 최소값을 정의할 수 있고, 곧 outlier의 최대 비율을 의미한다.
Comments