4 min to read
RBF Kernel
RBF Kernel
RBF Kernel - SVM
Introduction
비선형 데이터 분포를 다루는 문제에서 선형 분류는 한계를 지닌다. 실제데이터는 종종 입력 공간에서 선형적으로 구분되지 않으며, 이러한 경우 선형의 초평면으로는 적절한 분류를 할 수 없다.
이를 해결하기 위한 대표적인 접근인 Kernel Trick을 통해 이 문제를 해결해 보자.
Decision Function
SVM의 결정함수는 KKT + Lagrange 를 이용해 다음과 같이 도출되었다.
\[f(\mathbf{x}) = \sum_{i=1}^{N} \alpha_i y_i \langle \mathbf{x_i}, \mathbf{x} \rangle + b\]새로운 입력 x에 대해 모든 학습 샘플과의 내적을 계산하여 그 합으로 예측하는 구조이며, KKT를 통해 결국 support vector와의 코사인유사도(Cosine similarity) 만 확인하는 것을 확인하였다.
하지만 이는 선형일때의 경우이고 비선형데이터는 단순한 초평면으로 나누기 힘들다.
Kernel Trick
Kernel Trick은 입력데이터를 고차원 feature space로 embedding하여, 그 공간에서 데이터를 선형적으로 구분할 수 있도록 만드는 방법이다.
즉, 원래 공간에서 비선형 관계를 가진 데이터라도, 적절한 비선형 사상함수를 이용해 새로운 공간으로 옮기면
그 공간에서 다음과 같은 선형 결정 경계(Linear Decision Boundary) 를 적용할 수 있다.
\[f(x) = w^T \phi(x) + b\]하지만 실제로 이를 명시적으로 계산할때 차원이 매우 커지기 때문에 계산 비용이 폭발적으로 증가한다.
이 때문에, kernel trick은 두 벡터의 내적을 커널 함수로 대체한다.
\[K(x_i,x_j)= \langle\phi(x_i), \phi(x_j)\rangle\]이러한 커널 함수를 사용해 결정함수를 다음과 같이 쓸 수 있다.
\[f(\mathbf{x}) = \sum_{i=1}^{N} \alpha_i y_i K(\mathbf{x_i},\mathbf{x}) + b\]이 방식으로 고차원에서도 내적을 직접 계산하지 않고도 비선형 데이터를 분리할 수 있다.
커널함수로는 Polynomial, sigmoid, RBF 등이 있다.
이중 가장 많이 쓰이는 RBF커널에 대해 알아보자.
RBF Kernel
RBF Kernel (Radial Basis Function Kernel) 은 가장 널리 사용되는 비선형 커널이다.
RBF Kernel은 두 벡터간 의 유클리드 거리(Euclidean distance) 를 기반으로, 입력 벡터의 유사도를 다음과 같이 계산한다.
\[K(\mathbf{x_i}, \mathbf{x_j}) = \exp\left(-\gamma \|\mathbf{x_i} - \mathbf{x_j}\|^2\right)\]· Measures similarity between two points
· Close points → value near 1
· Distant points → value near 0
Taylor Series Expansion
RBF kernel의 형태는 다음과 같이 생겼다.
\[K(\mathbf{x_i}, \mathbf{x_j}) = \exp\left(-\gamma \|\mathbf{x_i} - \mathbf{x_j}\|^2\right)\]그리고 여기서 유클리드 제곱항으로 다시 써보면
\[\|\mathbf{x_i} - \mathbf{x_j}\|^2 = \|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2 - 2\mathbf{x_i}^T\mathbf{x_j}\]따라서 식은 다음과 같이 된다.
\[K(\mathbf{x_i}, \mathbf{x_j}) = \exp\left(-\gamma(\|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2)\right) \cdot \exp\left(2\gamma \mathbf{x_i}^T\mathbf{x_j}\right)\]이제 두 번째 항을 테일러 급수로 전개해보자.
기본적으로 지수함수의 테일러급수는 다음과 같다.
\[e^z = \sum_{n=0}^{\infty} \frac{z^n}{n!}\]여기서 z에 주어진 식을 대입하면
\[\exp(2\gamma \mathbf{x_i}^T \mathbf{x_j}) = \sum_{n=0}^{\infty} \frac{(2\gamma)^n}{n!} (\mathbf{x_i}^T \mathbf{x_j})^n\]따라서 전체 커널은 다음과 같이 확장된다.
\[K(\mathbf{x_i}, \mathbf{x_j}) = \exp\left(-\gamma(\|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2)\right) \sum_{n=0}^{\infty} \frac{(2\gamma)^n}{n!} (\mathbf{x_i}^T \mathbf{x_j})^n\]이를 다 전개해보면 다음과 같이 쓸 수 있다.
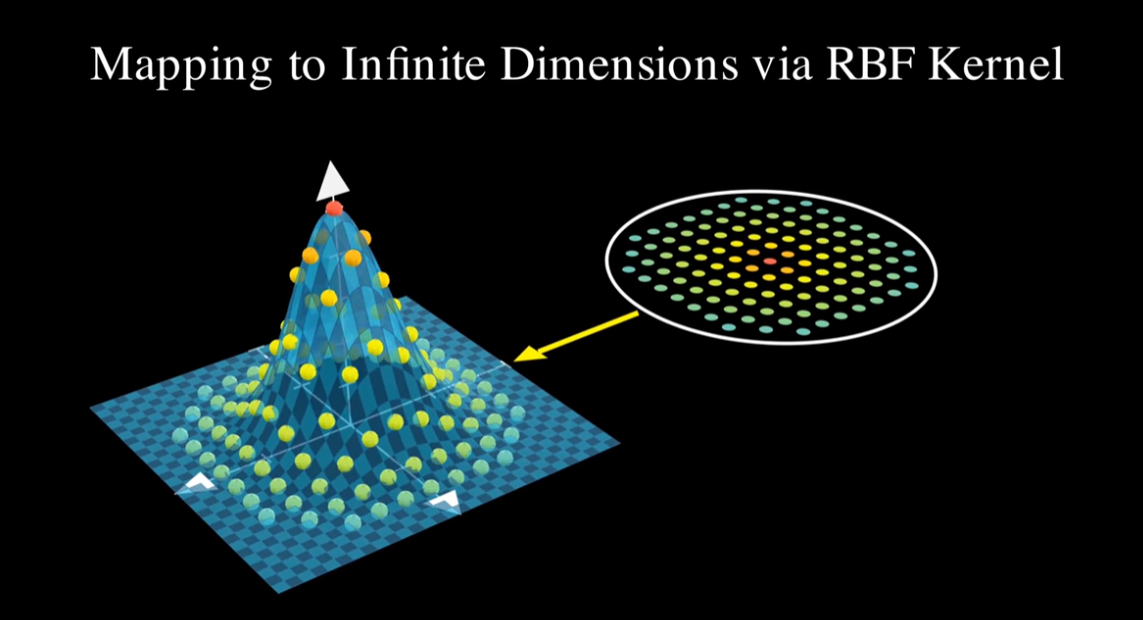
\[\exp\!\left(-\gamma(\|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2)\right) = 1 - \gamma(\|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2) + \frac{\gamma^2}{2!}(\|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2)^2 - \frac{\gamma^3}{3!}(\|\mathbf{x_i}\|^2 + \|\mathbf{x_j}\|^2)^3 + \cdots\]첫번째 항은 Constant dimension, 두번째는 Linear dimensions, 세번째는 Quadratic, 네번째는 Cubic 이런식으로 무한차원으로 나오는 것을 볼 수 있다.
이를통해 RBF Kernel은 무한차원 feature space에서의 내적을 암묵적으로 계산하고 있다는 것을 보여준다.
그리고 이런 무한차원성은 어떤 데이터 형태에도 무한차원으로 mapping이 가능해 비선형 관계를 표현할 수 있음을 보여준다.
Decision Function - The RBF Kernel
RBF Kernel을 기존 Decision fucntion에 넣으면 다음과 같이 쓸 수 있다.
\[f(\mathbf{x}) = \sum_{i=1}^{N} \alpha_i\, y_i \, \exp\!\left(-\gamma \,\|\mathbf{x_i}-\mathbf{x}\|^{2}\right) + b\]마찬가지로 입력 x에 대해 학습데이터(support vector)와의 유사도(similarity)를 계산한다.
· Close in feature space → High K values
· Distant in feature space → Low K values
RBF 커널의 최대 장점은 굳이 무한 차원 계산없이 feature space간의 내적을 해주는 커널 함수만 사용하면 된다는 것이다
The Gamma Parameter
RBF Kernel에서 γ (gamma) 는 거리 척도의 민감도(the influecne radius) 를 조절하는 하이퍼 파라미터이다.
· Small γ : Wide influence
· Large γ : Local influence
from sklearn.svm import SVC
model = SVC(
C=1.0, # 규제(regularization) 강도
kernel='rbf', # 커널 종류: 'linear', 'poly', 'rbf', 'sigmoid'
degree=3, # 다항식 커널에서 차수 (poly 전용)
gamma='scale', # RBF/poly/sigmoid 커널의 감마값 ('scale', 'auto', float 가능)
coef0=0.0, # 다항식/시그모이드 커널의 상수항
shrinking=True, # 수축 히스틱(heuristic) 사용 여부
probability=False, # 확률 추정(predict_proba) 사용 여부
tol=1e-3, # 수렴 기준
cache_size=200, # 커널 캐시 크기(MB)
class_weight=None, # 클래스 불균형 시 가중치 부여
verbose=False, # 학습 과정 출력 여부
max_iter=-1, # 최대 반복 수 (-1은 무제한)
decision_function_shape='ovr', # 다중분류 방식 ('ovo' or 'ovr')
break_ties=False, # 다중분류 시 동점 처리 여부
random_state=None # 난수 시드
)
여기서 gamma를 조절해서 조절할 수 있다.
Comments