January 24, 2026 3 min to read

Ensemble Learning, Random Forests

Random Forests

Introduction

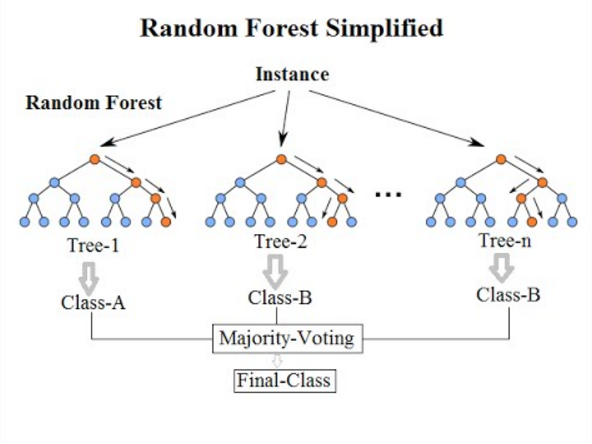
Random Forests(RF) 는 Classfication, Regression 등 다양한 분석에서 활용되는 Ensemble Learning 기법중 하나로, 이름에 Forest가 들어갔듯이 여러개의 Decision Tree로 구성되어 있다. Bagging 기법과 Random Space 기법으로 기존 Decision tree에서의 overfitting 문제를 해결하였으며 빠르고 높은 정확성을 갖는 알고리즘으로 많이 사용되고 있다.

Motivation on RF

Decision Tree

Tree는 계층 구조로 이루어진 node들과 edge들의 집합으로 이루어져 있으며, Graph와 달리 모든 node는 단 한개의 incoming edge만을 가지고 있다. 그리고 Decision Tree는 말그대로 결정을 내리기위해 사용하는 tree로 예시로 다음과 같은 재밌는 예시가 있다.

간단한 문제는 직접 parameter들을 설정해서 할 수 있지만, 복잡한 문제는 구조와 변수들을 학습시켜서 사용할 수 있다.

Motivation

Decision Tree는 input space를 piecewise해서 서로 다른 상수를 내는 non-linear 모델이기 때문에 입력에 따라 다른 규칙(비선형 경계)를 쉽게 표현할 수 있지만, 유연한 만큼 일반화 성능이 떨어진다는 점과 계층적 접근방식이기 때문에, 에러또한 계속해서 전파된다는 단점이 존재한다.

RF는 Bagging기법과 Random Space 기법으로 기존 decision tree의 단점을 극복하여 좋은 일반화 성능을 이끌어 낸다. 여담으로 본 알고리즘을 제시한 Leo Breiman의 논문에는 Random Forest’s’ 라고 적혀 있으나, 통상적으로 Random Forest로 많이 쓴다.

Random Forests

앞서 언급했듯이, RF는 2가지의 핵심기법인 Bagging과 Random Space를 사용한다.

Algorithm

(a) 학습데이터로부터 N크기의 bootstrap(복원추출) sample Z를 뽑는다.

이때 복원 추출 원리에 따라 약 63.2%의 서로다른 샘플이 포함되며, 나머지는 OOB에 들어간다.

(b) 각 bootstrap 샘플로 RF의 decision tree T를 만들고 분할 불가능한 최소의 노드 크기인 n에 도달할때까지 다음 과정을 재귀 반복한다.

전체 p개의 변수들에게서 m개의 변수를 랜덤하게 뽑는다 (변수 제약)

선택된 m개 변수사이에서 최적의 분할 변수와 분할 지점을 고른다

해당 기준에 따라 2개의 자식노드(doughter nodes)로 분할한다.

위 과정을 B개의 indivitudal learner에 대해 독립적으로 반복하여 RF를 구성한다.

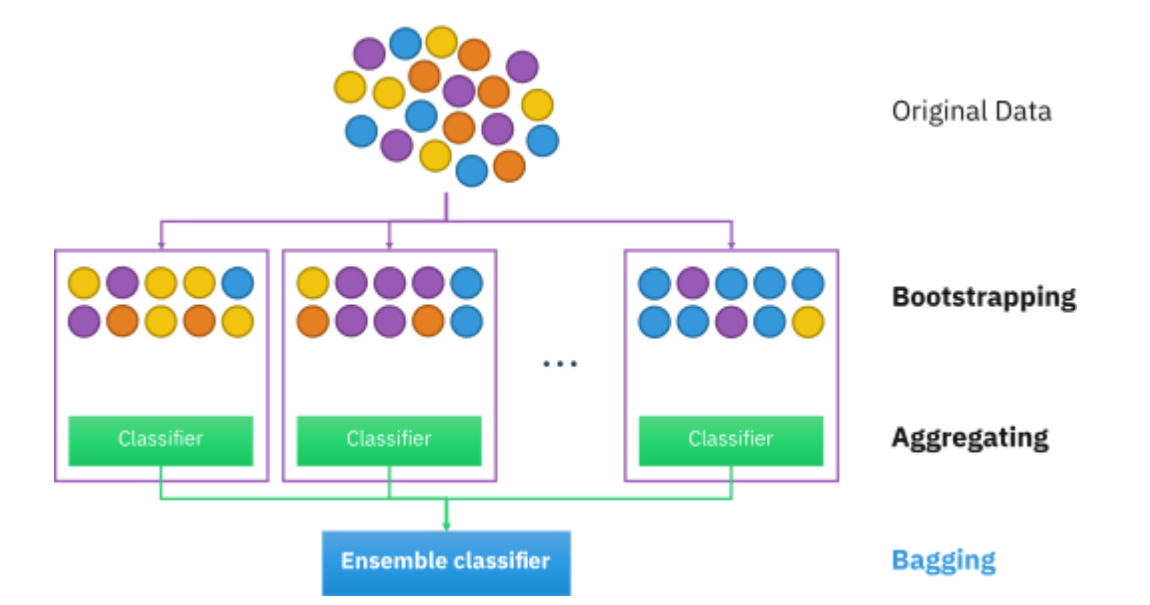
Bagging

RF에서 핵심은 랜덤할때 뽑을때 Bagging을 사용한다는 것이다. Decition tree의 특징은 Reculsive partitioning을 한다는 것인데, 원래는 변수가 100개 있다고 했을때,100개의 경우의 수를 다 탐색해야 하지만, RF는 모든 변수를 사용하는 것이 아닌, 일부만 사용해서 tree를 구성한다.

일부만 사용한다는 점에서 성능이 떨어질 것 같지만, decision tree의 data를 제한함으로써 diversity를 확보하고 이를 통해 성능을 향상시키는 것이 RF의 mechanism이다.

Generalization Error

RF의 각각의 tree들은 pruning(가지치기)를 하지않으면 overfitting될 수 있다.

Tree들이 충분이 있다고 가정할때, RF의 기대손실(the generalization error)의 상한은 다음과 같다.

Notation

p : 개별 tree들의 상관계수들에 대한 평균, s : margin function

\[Generalization \ Error \leq \frac {\bar p(1-s^2)}{s^2}\]

이는 곧 s의 크기를 키우면, 기대손실이 줄어들고 이는 곧 각각의 classifier들의 정확도가 향상된다. 또한 상관관계가 낮을수록 기대손실이 줄어든다.

Variable Importance

RF는 OOB를 통해 변수의 중요도를 산출할 수 있다. 원래의 dataset의 OOB error를 계산하고, i번째 변수를 섞은 뒤 다시 OOB를 계산한다. 그리고 이것의 차이에 대한 평균과 표준편차를 기반으로 변수의 중요도를 산출할 수 있다.

만약 i번째 변수가 split에 사용되지 않았다면, 섞기 전 후의 OOB error가 비슷하기 때문에 중요도가 낮다고 판단할 수 있고, 반대로 자주 사용된다면 변수를 섞은 후에 중요한 변수가 이상한 값으로 대체되어 예측력이 망가지기 때문에 중요도가 높다고 판정할 수 있는것이다.

즉 중요도가 높다면 Random permutation의 전 후의 OOB Error가 크게 나야 하고 편차가 적어야 한다. m번째 tree에서 i번째 변수에 대한 OOB Error차이를 다음과 같이 쓸때,

\[d_i^m = p_i^m - e_i^m\]

평균과 분산은 다음과 같이 쓸 수 있다.

\[\bar d_i = \frac{1}{m}\sum_{i=1}^m d_i^m, \ s_i^2 = \frac{1}{m-1}\sum_{i=1}^m(d_i^m - \bar d_i)^2\]

그리고 i번째변수의 중요도는 다음과 같이 정의할 수 있다. \(v_i = \frac{\bar d_i}{s_i}\)