4 min to read
Support Vector Data Description
SVDD

Support Vector Data Description
Introduction
SVDD (Support Vector Data Description) 는 정상 데이터만을 학습해 정상 데이터가 분포하는 영역을 최대한 작게 포괄하는 hypersphere를 찾는 방법론이다.
정상 데이터만을 학습하여 결정함수를 도출하는 supervised learning이며, 영역 외부의 점들을 이상치로 탐지하는 알고리즘이다.
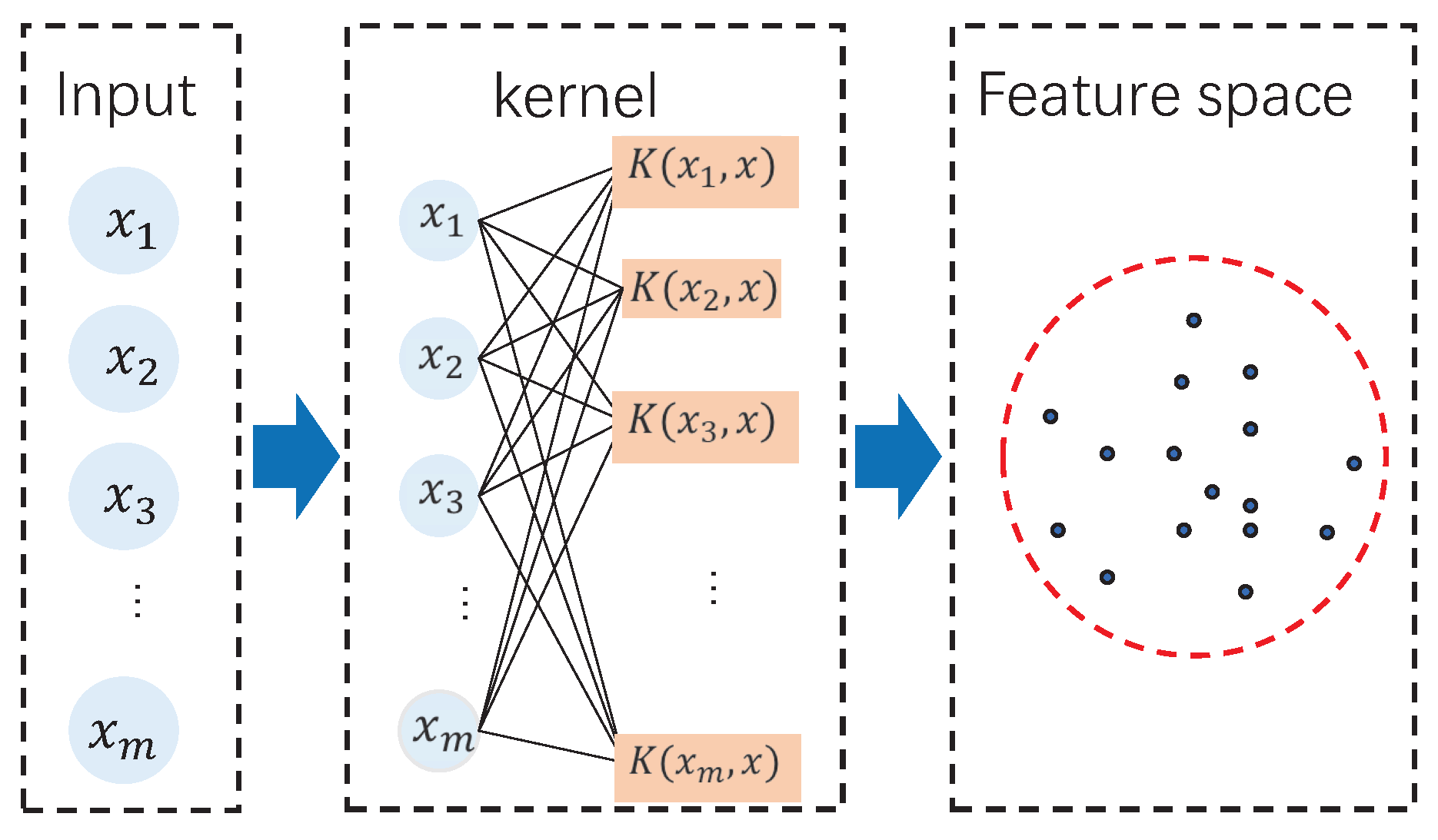
SVM, OCSVM과 마찬가지로 RBF 커널 등 Kerner Trick을 적용함으로써 비선형 구조의 데이터도 고차원으로 매핑시켜 효율적으로 탐지해낼 수 있다.
Support Vector Data Description
SVM이 두 support vector간의 margin, OCSVM이 원점과 정상데이터 간의 margin을 최대화 시켰다면, SVDD는 중심 a와 반지름 R을 가진 hypersphere에서 R을 최소화 시킴으로 최소한의 영역을 찾아낸다.
Hard-Margin SVDD
반지름 R의 최소화
결국 목적함수인 R에 대한 최소화 식은 다음과 같이 표현할 수 있다
\[\min_{R,a} R^2\]데이터 위치에 대한 제약식
정상데이터는 반지름 R안에 hypersphere안에 들어가야 하므로 다음과 같이 표현할 수 있다
\[s.t. \ \|x_i-a\|^2\leq R^2 \ , \forall i\]따라서 다음과 같이 convex optimization problem으로 정의할 수 있다 .
\[\min_{R,a} R^2\] \[s.t. \ \|x_i-a\|^2\leq R^2 \ , \forall i\]Lagrange + KKT Condition
inequality contraints optimization 문제이므로 lagrange + KKT Condition으로 최적화를 한다.
Stationarity
Complementary slackness
\[\alpha_i(\|x_i-a\|^2 - R^2) = 0\]α에 대한 값 해석
SVM계열 알고리즘과 마찬가지로, α가 양수일경우 제약 부등식이 0이 되고 이는 곧, support vector를 의미한다. 그리고 α가 =일경우 제약 부등식이 양수이므로 이는 곧, 내부점을 의미한다.
α = 0, 제약식 = 0 일 경우 경계점이지만 최적화에 아무런 영향을 주지않는 의미없는 점이다.
Soft-Margin SVDD
모든 데이터를 완벽하게 포괄할 수는 없기 때문에 마찬가지로 슬랙변수 ξ(xi)를 넣음으로써, 약간의 오분류를 허용하게 할 수 있다.
SVDD는 모든 데이터를 hypersphere에 다 넣을 수 있지만, 몇개의 이상치가 hypersphere를 왜곡시켜, 성능을 급격하게 떨어뜨릴수 있기 때문에, 오분류를 허용함으로써, 성능을 올릴 수 있다.
반지름 최소화
\[\min_{R,a,\xi} R^2 + C\sum_i^n\xi_i\]데이터 위치에 대한 제약식
\[s.t. \ \|x_i-a\|^2\leq R^2+\xi_i \ , \ \xi_i \geq 0\]Lagrange + KKT Condition
\[L(R,a,\xi,\alpha,\gamma)=R^2 + C\sum_i\xi_i+\sum_i\alpha_i(\|x_i-a\|^2 - R^2-\xi_i)-\sum_i\gamma_i\xi_i\]Stationarity
\[\frac{\partial L}{\partial a} = 0 \ \rightarrow \ a = \sum_i\alpha_ix_i\] \[\frac{\partial L}{\partial R} = 0 \ \rightarrow \ \sum_i\alpha_i = 1\] \[\frac{\partial L}{\partial \xi_i} = 0 \ \rightarrow \ \alpha_i + \gamma_i = C\] \[\therefore 0 \leq \alpha_i \leq C\]Complementary slackness
\[\alpha_i(\|x_i-a\|^2 - R^2) = 0\] \[\gamma_i\xi_i = 0\]α,γ 에 대한 값 해석
\[Case \ 1: \ \alpha_i = 0 \ \rightarrow \ 경계안쪽, \ 정상점\] \[Case \ 2: \ 0<\alpha_i<C \ \rightarrow \ 경계점, Support \ Vector\] \[Case \ 3: \ \alpha_i = C \ \rightarrow \ 외부점, \ outlier\ 후보, \ Support \ Vector\]해석은 OCSVM과 비슷하다. case 1, 2는 Hard-Margin과 동일하다.
case 3같은 경우에는 α가 C (양수)이기 때문에 제약식은 0이 되고, 이는 곧 서포트 벡터를 의미한다.
그리고 KKT에서 도출된 α + γ = C 조건으로 인해, α가 C는 곧 γ = 0이되고, γ가 0이면 ξ가 양수이기 때문에 이상치 후보이자 서포트벡터가 된다
Decision Function
위에서 구한 식을 대입함으로써 결정함수를 구할 수 있다
\[\begin{aligned} f(x) &= x^\top x - 2 \sum_{i=1}^n \alpha_i x^\top x_i + \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j x_i^\top x_j - R^2 \end{aligned}\] \[\begin{cases} f(x) \le 0 & \text{normal} \\ f(x) > 0 & \text{anomaly} \end{cases}\]SVDD & OCSVM
SVDD와 OCSVM은 경계는 다르게 생겨도, 모든 데이터가 단위 벡터로 정규화 되었다면, 둘은 서로 수학적으로 동치이다.
Kernel Trick
비선형 구조같은 경우에는 고차원 매핑으로 해결할 수 있다. 하지만 고차원 매핑의 계산량을 해결하기 위해 Kernel Trick을 사용한다.
가장 많이 사용하는 Kernel로는 RBF Kernel이 있다. 하지만 거리기반 함수이기 때문에, 마찬가지로 이론상 무한차원 매핑이 가능하지만 실제로 무한차원으로 보낼시 차원의 저주로 인해 성능이 급격하게 떨어진다.
Minimize total variance
Hard-Margin에서는 중심 c가 평균을 의미하고 Soft-Margin에서는 support vector 기반 가중 평균을 의미한다.
\[c = \sum_i \alpha_i x_i\]이때 공분산은 다음과 같이 정의할 수 있다
\[\Sigma_\alpha = \sum_i \alpha_i (x_i-c)(x_i - c)^T\]위 정의에 따라 다음과 같이 유도할 수 있다
\[tr(\Sigma_\alpha) = tr(\sum_i \alpha_i (x_i-c)(x_i - c)^T)\] \[= \sum_i \alpha_i tr((x_i-c)(x_i-c)^T)\]그리고 외적의 trace = 벡터의 제곱 norm을 이용하면
\[tr((x_i-c)(x_i-c)^T) = \|x_i-c\|^2\]따라서 공분산 행렬의 trace 를 의미하고 이는 분산의 총량을 의미한다.
SVDD는 위 식을 최소화하는 것은 분산의 총량의 최소화하는 것과 동치이다.
Single-center Assumption
SVDD의 가장 큰 단점은 중심가정을 한다는 것이다. 정상데이터가 하나의 중심이라고 가정하기 때문에, multimodal의 경우에 부적합하다. 이를 해결하기 위해 다양한 방법론이 존재한다.
그중 하나의 중심으로 끌어내는 잠재공간을 찾아내는 Deep SVDD 방법론이 주목받고 있다.
Reference
[1] L. Ruff, J. R. Kauffmann, R. A. Vandermeulen, G. Montavon, W. Samek, M. Kloft, and K.-R. Müller,
“Deep Semi-Supervised Anomaly Detection,”
in Proc. 8th Int. Conf. Learn. Represent. (ICLR), Addis Ababa, Ethiopia, 2020.
[2] D. M. J. Tax and R. P. W. Duin,
“Support vector data description,”
Machine Learning, vol. 54, no. 1, pp. 45–66, Jan. 2004.
Comments