13 min to read
Support Vector Machine
SVM
Support Vector Machine (SVM)
ABSTRACT
서포트 벡터 머신(Support Vector Machine, SVM) 은 고차원 데이터에서도 강력한 분류 성능을 보이는 대표적인 지도학습 기법이다.
Random forest, NeuralNet과 더불어 가장 많이 사용되는 ML기법으로 관련 전공자라면 한번쯤은 들어봤을법한 기법이다.
SVM의 핵심 아이디어는 주어진 데이터들을 가장 넓은 마진(margin) 을 확보할 수 있도록 분리하는 초평면(hyperplane)을 찾는 것이다.
이때 초평면과 가장 가까이 위치한 데이터 점들을 서포트 벡터(support vectors) 라 부르며, 이들이 결정 경계(decision boundary)를 정의하는 데 핵심적인 역할을 한다.
선형적으로 분리 가능한 경우에는 최대 마진 분류기를 통해 간단히 경계를 찾을 수 있지만, 실제 데이터는 잡음(noise)과 중첩(overlap)을 포함하는 경우가 많다.
이를 위해 SVM은 소프트 마진(soft margin) 기법과 커널 함수(kernel trick) 를 도입하여, 선형적으로 구분 불가능한 문제도 고차원 특징 공간(feature space)으로 사상(mapping)함으로써 효과적으로 분리할 수 있도록 확장되었다.
SVM은 이론적으로 견고한 최적화 문제(Lagrangian dual formulation) 를 기반으로 하며, 높은 일반화 성능과 과적합 억제 능력으로 인해 텍스트 분류, 이미지 인식, 생체 데이터 분석 등 다양한 응용 분야에서 널리 활용되고 있다.
Introduction
다음과 같이 데이터를 2가지로 분류할때 어떤 직선이 더 잘 나눴는지 생각해보자.
대다수의 사람이 파란색 직선이라고 하겠지만, 엄밀히 말하면 둘다 잘 분류는 하고있다.
하지만 파란색 직선이 더 잘 나눴다고 하는 근거는 빨간색 직선에 비해 한쪽으로 치우쳐지지 않고 적절히 잘 배치 되었기 때문이다.
이걸 Machine Learning 관점에서 봤을때, train data를 잘 학습해 test data에 잘 적용되어야 한다.
즉, 학습데이터는 물론, 새로운 데이터에도 잘 대응해야 하는 generalization performance가 필요하다.
이러한 관점에서 봤을때, 가장 큰 틈을 가지도록 하는 선, 또는 최소거리가 최대가 되는 선이 더 좋은 선이라고 볼 수 있다.
이제 이 글의 주제인 Support Vector Machine에 대해 알아보자.
방금 생각해봤던 빨간직선, 파란 직선을 SVM에서 결정 경계(초평면, hyperplane) 이라 부른다.
그리고 더 좋은선의 조건인 가장 큰 틈을 margin 이라 부르고, 위 결정 경계와 가장 가까운 데이터 포인트들을 support vector라고 부른다.
즉, SVM은 이 margin을 최대화 할 수 있는 hyperplane을 찾는 알고리즘이라 할 수 있다.
Description of SVM
SVM의 핵심은 고차원에서 두개의 그룹을 가장 넓게 분리하는 가상의 초평면(hyper plane)을 찾아내는 것이다.
위 그림에서 각 그룹에서 가상의 구분선 까지의 거리가 가장 짧은 데이터를 support vector 라고 부른다.
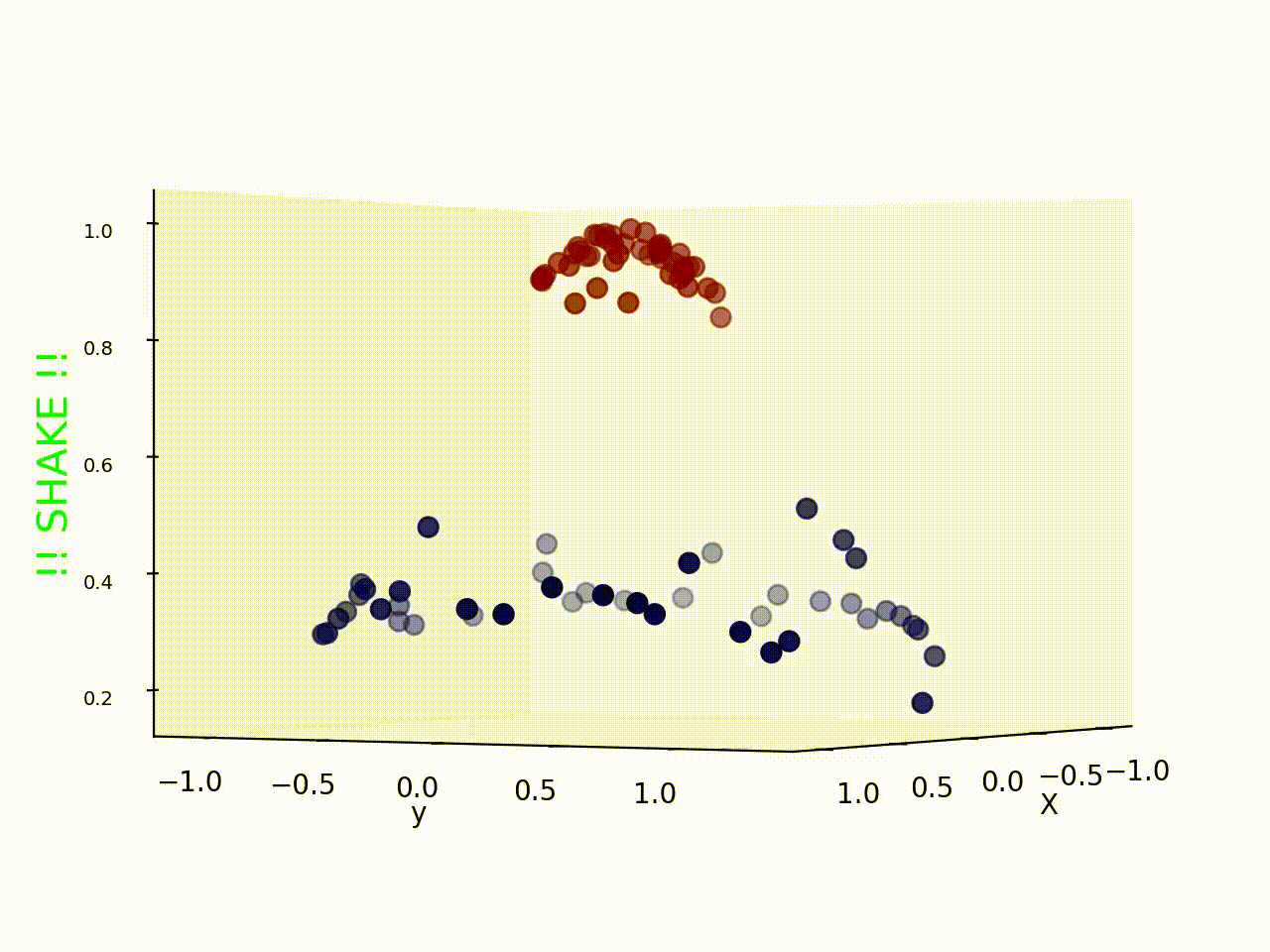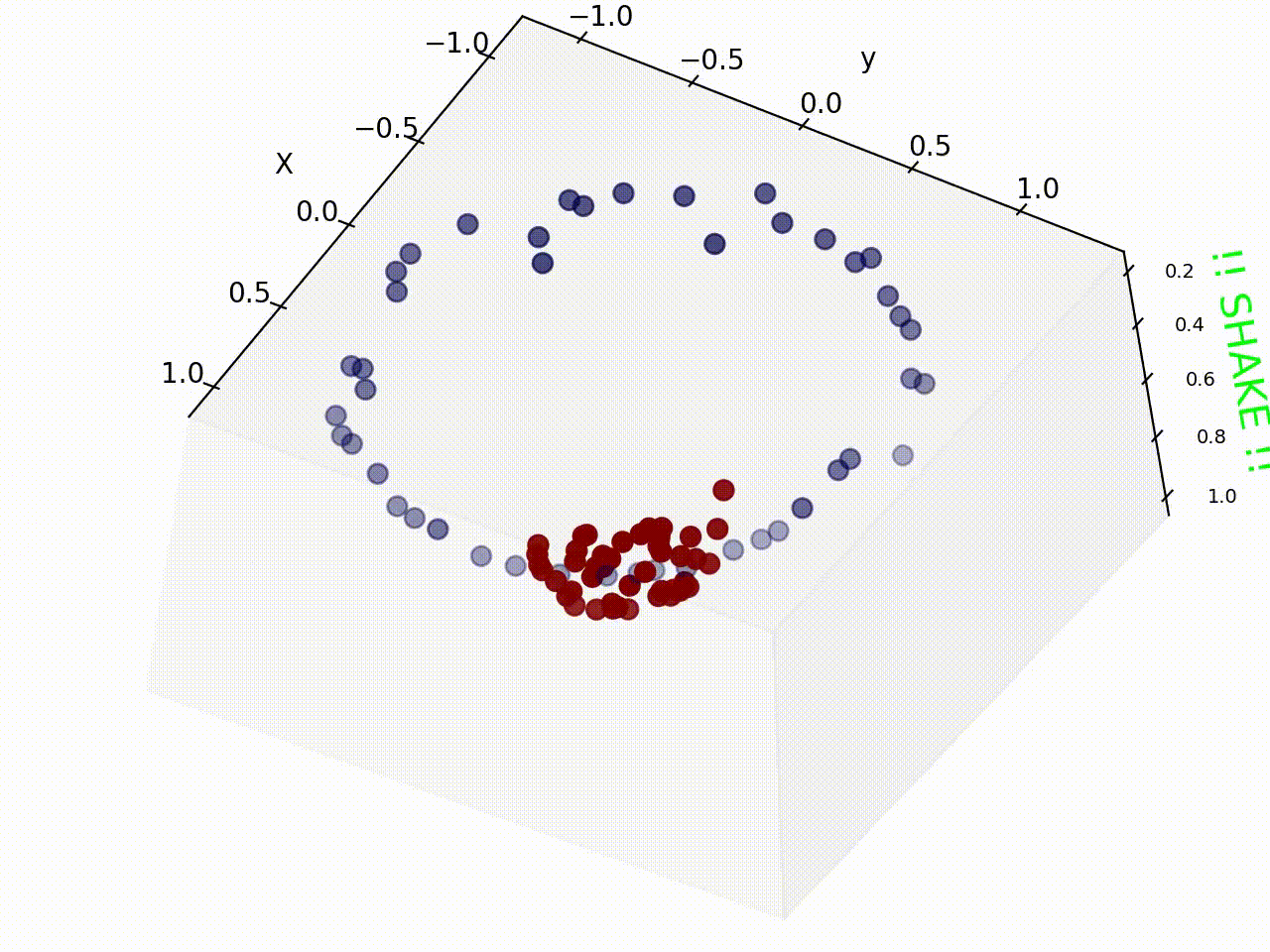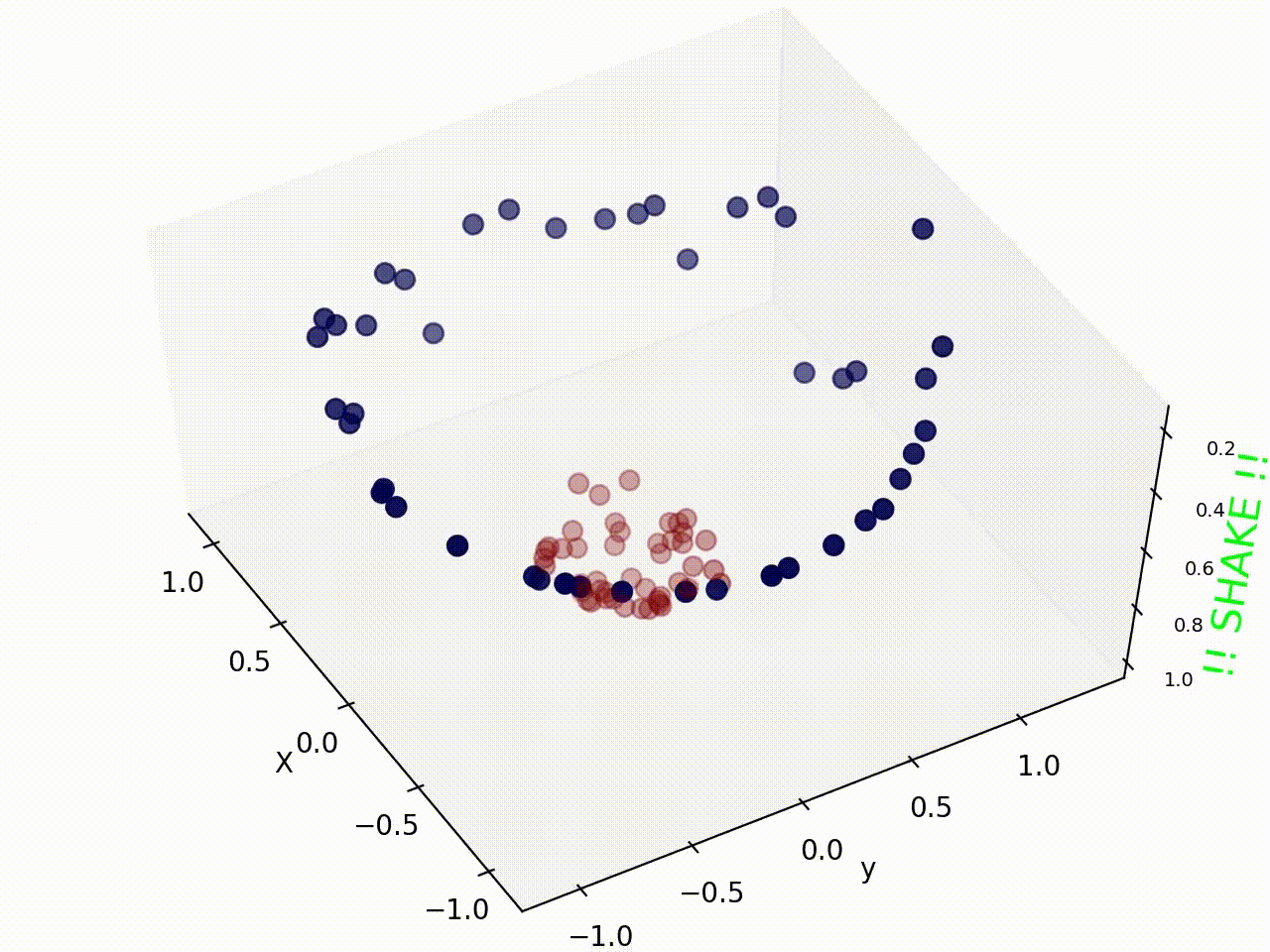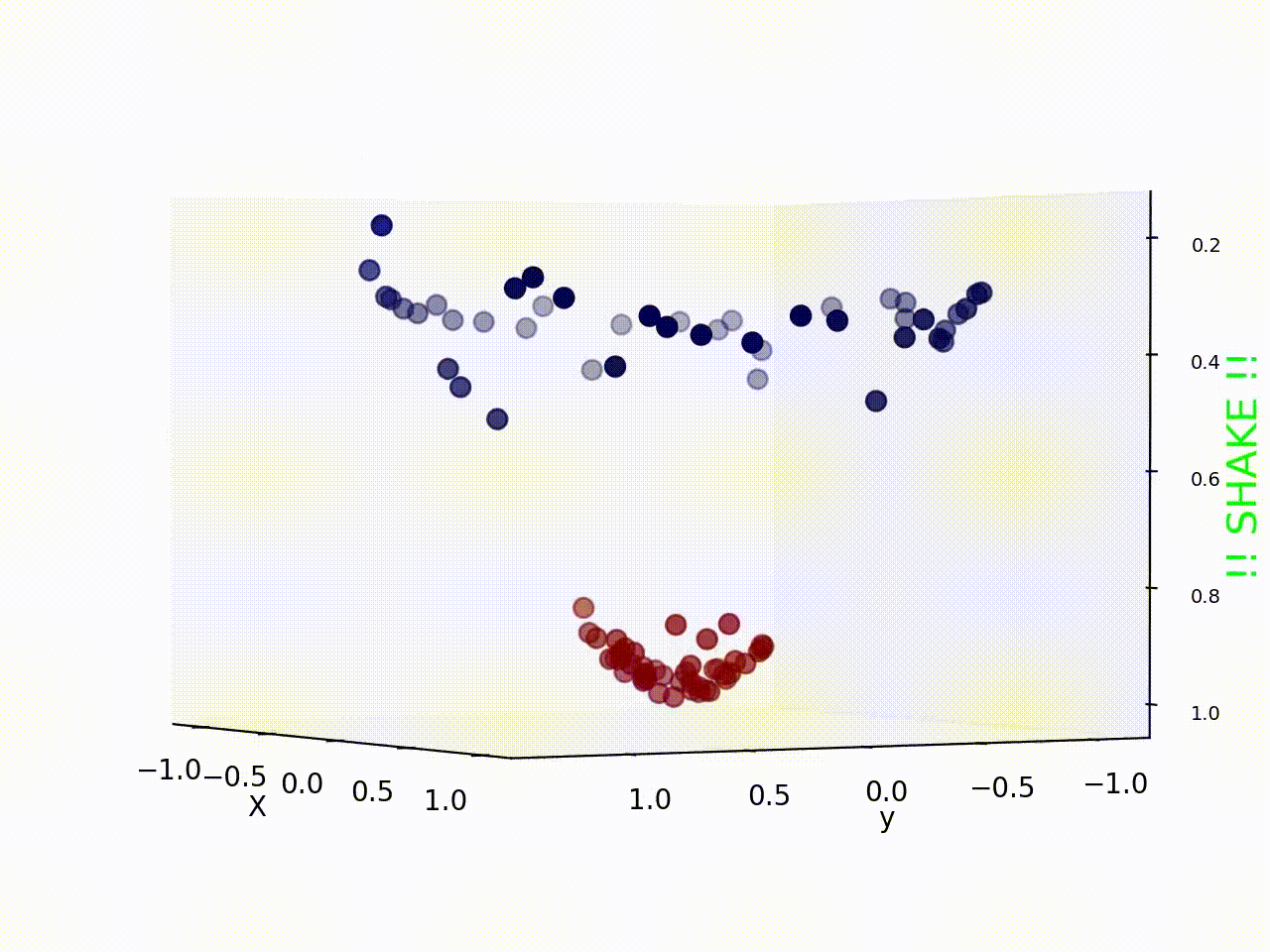
여기서 위 그림처럼 선형 데이터일 경우 직선을 그어 두가지 그룹을 분리 할 수 있지만, 현실 세계와 같은 비선형 데이터는 위 그림처럼 직선으로 나누기 쉽지 않다.
하지만 Kerner trick 을 사용해 이런 Non-linear data 또한 아래 그림과 같이 SVM을 사용해 분류시킬 수 있다.
이제 SVM의 원리와 다양한 종류에 대해 알아보자.
Mathematical Principles of SVM
이전 통계적 기법인 MCD는 선형대수 중심된 이론이였다면, SVM은 다변수 미적분에서 최적화 기법에 가깝다.
다음과 같은 SVM이 주어졌다고 생각해보자
이때 결정경계는 일차함수 형태로 있기 때문에, 수학적으로 표현하면 다음과 같다.
\[w^{T}x + b = 0\]이를 보기쉽게 element 표현으로 적으면 다음과 같이도 표현할 수 있다. (2차원 이므로 basis 2개)
\[w_{1}x_{1} + w_{2}x_{2} + b = 0\]이때 전개할 때 보기쉽게 빨간데이터 범주를 결정경계보다 +1(혹은 그 이상)이라 하고 파란 데이터 범주를 -1(혹은 그 이하)라고 해보자.
그럼 범주를 다음과 같이 쓸 수 있다.
빨간데이터 :
\[w_{1}x_{1} + w_{2}x_{2} + b \geq 1\]파란데이터 :
\[w_{1}x_{1} + w_{2}x_{2} + b \leq -1\]그럼 margin의 크기는 다음과 같이 된다.
\[\text{Margin} = \frac{2}{\|w\|} = \frac{2}{\sqrt{w_1^2 + w_2^2 + \cdots + w_d^2}}\]위의 예시는 2차원이므로 다음과 같이 쓸 수 있다.
\[\text{Margin} = \frac{2}{\sqrt{w_1^2 + w_2^2}}\]여기서 분자인 2는 우리가 경계조건을 1,-1로 놓았기때문에 나온 숫자였지만 scaling을 통해 분자가 2가 나옴을 유도할 수 있다..
hyperplane scaling
\[w^{T}x + b = 0\] \[(cw)^Tx + cb = 0\] \[c(w^Tx + b) = 0\]이처럼 어떠한 상수를 곱해도 초평면이 나오는 것을 알 수 있다.
그리고 margin 공식은 단순한 두 직선 사이의 거리 공식이다.
Remind: distance between two line
위 공식을 경계조건을 통해 대입해 보면 다음과 같이 계산할 수 있다.
\[d = \frac{|(b-1) - (b+1)|}{\sqrt{w_1^2 + w_2^2}} = \frac{2}{\sqrt{w_1^2 + w_2^2}}\]따라서 우리의 목표인 margin maximization을 위해서는 결국 분모를 최소화 시키면 되고,
이는 곧 norm을 최소화 시키면 된다.
SVM에서는 계산의 편의를 위해 다음을 최소화 하는 방향으로 식을 세운다.
\[(1/2)\|w\|^2\]그리고 빨간데이터와 파란데이터를 동시에 만족시키는 조건은 다음과 같은 식 하나로 표현할 수 있다.
\[y(w_{1}x_{1} + w_{2}x_{2} + b) \geq 1\]y에 각각 1과 -1을 넣어보면 우리가 설정한 경계조건이 나옴을 직관적으로 알 수 있다.
정리해 보면, 다음과 같은 문제로 정의할 수 있다.
“다음과 같은 경계조건(constraints)에서의 margin의 최대를 구하여라”
이는 곧 제약조건의 최대 최소 (최적화) 문제라고 볼 수 있다.
SVM의 최적화는 이런 경계조건에서의 최적화문제에서 많이 쓰이는 방법인 Lagrange multiplier method를 사용해서 해결한다.
라그랑즈 승수법에 대한 자세한 내용은 다음 post에 담겨있다.
간략하게 설명하면 라그랑즈 승수법은 함수의 등고면과 제약곡면이 접할때
즉 gradient가 평행 할때 최대 최소를 갖는 것을 의미한다.
이를 우리가 풀어야 할 최적화 문제로 문제정의를 하면 다음과 같이 쓸 수 있다
\[L(w, b, \alpha) = \frac{1}{2}\|w\|^2 - \sum_i \alpha_i \big[ y_i (w^T x_i + b) - 1 \big]\]일단 해석을 해보면 앞에 1/2 norm(w)^2은 margin의 최대화 즉, 목적함수 이다.
그리고 뒤 두번째 항은 constraints condition을 만족하는 정도이고 α는 라그랑즈 상수,
원래의 형태에서 lambda에 해당한다.
그럼 sigma는 뭐냐,
SVM 제약조건은 각 데이터마다 존재하기 때문에 하나씩 붙여서 더해주어야 한다.
그러면 여기서 support vector의 제약조건만 계산하면 되는데 왜 모든 데이터에 다 정의하는지에 대한 의문을 가질 수 있다.
이유는 처음에는 누가 support vector인지 모르기 때문에, 모든 데이터에 대해 constraints를 걸어야 한다.
그리고 이후에 이 알고리즘에 핵심인 Karush-Kuhn-Tucker (KKT) conditions을 사용한다.
KKT 조건은 다음과 같다
① Stationarity
② Primal feasibility
③ Dual feasibility
④ Complementray slackness
원래 풀던대로 부등식에서 최대 최소는 경계조건에서의 최대 최소값과 내부 점에서 최대 최소값을 찾아서 비교하면 되지 않을까? 하는 의문을 가질 수 있지만,
단순한 작은 문제에서는 쉬울 수 있지만, 일반 최적화에서는 KKT 조건을 사용했을때 경계와 내부를 더 체계적이고 자동화 된 방식으로 풀 수 있다.
다시 본론으로 돌아와 KKT조건을 이용해 해결해 보자
간단한 계산을 위해, 전체 데이터가 아닌 두개의 서포트 벡터로 예시를 들어보자.
그리고 예시와 함께 일반화된 공식도 해석해보자.
여기서 각 서포트 벡터 2개에 대한 값을 넣어주면 다음과 같이 쓸 수 있다.
\[L = \frac{1}{2}\big(w_{1}^2 + w_{2}^2\big) - \alpha_{1}\big[y_{1}(w_{1}x_{11} + w_{2}x_{12} + b) - 1\big] - \alpha_{2}\big[y_{2}(w_{1}x_{21} + w_{2}x_{22} + b) - 1\big]\]이제 KKT 조건을 사용해 최소값을 구해보자.
KKT 조건 1 : Stationarity (정지조건)
unconstrained라면 극값 조건은 우리가 흔히 아는 기울기가 0인 곳이지만,
우리는 부등식이라는 constraints condition이 있기 때문에 경계에 걸려서 더 못내려가는 상태를 찾는 것이고, 최적점이 제약경계 내부에 있다면 상관없지만 제약조건 밖에 있을때는 더 못내려가 가게 막아줘야 한다.
이제 gradient를 구해보자. gradient는 각각의 변수에 대해 편미분을 해주면 된다.
그리고 더 내려가지못하게 막아줘야 하는 것은, gradient(경사)가 0임을 의미한다.
\[\nabla L = (\frac{\partial L}{\partial w_{1}}, \quad \frac{\partial L}{\partial w_{2}}, \quad \frac{\partial L}{\partial b}) = 0\] \[\frac{\partial L}{\partial w_{1}} = w_{1} - \alpha_{1} y_{1} x_{11} - \alpha_{2} y_{2} x_{21} = 0\] \[\frac{\partial L}{\partial w_{2}} = w_{2} - \alpha_{1} y_{1} x_{12} - \alpha_{2} y_{2} x_{22} = 0\]만약 2점이 아닌 여러점에 대해 식을 일반화 시키면 다음과 같이 쓸 수 있다.
\[\frac{\partial \mathcal{L}}{\partial w} = w - \sum_i \alpha_i y_i x_i = 0 \Rightarrow w = \sum_i \alpha_i y_i x_i\]여기서 서포트 벡터 각각의 점을 넣어주면 다음과 같이 나온다.
\[w_{1} = \alpha_{1} + \alpha_{2}\] \[w_{2} = \alpha_{1} + \alpha_{2}\]마찬가지로 b에 대한 값을 구하면 다음과 같다.
\[\frac{\partial L}{\partial b} = -\alpha_{1}y_{1} -\alpha_{2}y_{2} = 0\]이도 마찬가지로 2개의 변수가 아닌 일반화 시키면 다음과 같이 나온다.
\[\sum_i \alpha_i y_i = 0\]그리고 각각의 점을 대입하면
\[-\alpha_{1} + \alpha_{2} = 0\] \[\alpha_{1} = \alpha_{2}\]그리고 이를 w_1, w_2에 각각 대입하면 다음을 알 수 있다.
\[w_{1} = w_{2} = 2\alpha\]그리고 다음 KKT조건으로 넘어가기 전에 우리가 구한 일반화 식을 대입해 결정함수를 얻어낼 수 있다.
이렇게 얻어낸 식에서 부호를 통해 입력 데이터를 분류해 낼 수 있다.
그리고 이것이 후에 자세히 다룰 kernel과 연관되니 기억하자.
KKT 조건 2 : Primal feasibility(타당성) , KKT 조건 4 : Complementary slackness (상보조건)
조건 2 는 제약조건이 넘어가는 점이 없어야 한다는 조건이고, 조건 4는 라그랑즈 상수가 >= 0이여야 한다는 조건이다.
조건 2는 당연한거고 조건 4의 의미는 다음과 같다.
다음과 같이 잡았을때 내부에서는 다음과 같을 것이다.
\[y_i (w^T x_i + b) - 1 > 0\]그러면 처음 식이 0을 만족하기 위해서는 α가 0을 만족해야 한다.
그리고 경계로 잡으면 다음과 같이 되고
\[y_i (w^T x_i + b) - 1 = 0\]그러면 α는 0이 아니게 된다.
여기서 다음 KKT 조건으로 넘어가서 합쳐보자.
KKT 조건 2 : Primal feasibility(듀얼 타당성)
마지막 조건은 이전에서 구한 α는 양수라는 조건이다.
이전 post에서 언급은 안된 것 같지만, Lagrange 상수는 penalty 같은 존재이다.
제약 조건을 벗어나려고 하면 라그랑즈 상수 때문에, 값에서 배제 시킬 수 있다.
\[L(w,b,\alpha) = \frac{1}{2}\,\|w\|^2 - \sum_{i} \alpha_i \big[\, y_i (w^T x_i + b) - 1 \,\big]\]하지만 α 음수라면 오히려 값이 커져버려 제약 조건이 벗어나는 점이 최적점이 되어버린다.
결론적으로 라그랑즈 승수법에서 KKT조건을 이용한 최적화는 α가 최대이면서 w, b가 최소인 saddle point를 구하는 과정이다.
그리고 w,b를 primal 변수(margin을 위한 최소화)라고 하고 α를 dual 변수(제약 위반을 막음)라고 한다.
이제 마지막 정리를 해볼건데, 그전에 앞 조건을 다시 상기시켜보자.
우리는 margin을 최대화시키는 즉, norm(w)를 최소화를 시키는 w,b,α를 찾고 있고, L(x,b,α)의 안장점을 찾고있다.
여기서 KKT조건의 complementry slackness로 내부의 점에서는 α = 0이고 경계에서는 α > 0임을 알 수 있었다.
그러면, 경계의 점이 무엇을 의미할까
그 경계의 점이 support vector이다.
margin을 최대화시켜주는 margin의 경계에 있고, margin위에 있기때문에 α > 0인 지점 이는 곧, 다음 조건을 형성해서 풀어주면 된다.
\[y_i (w^T x_i + b) - 1 = 0\]이제 예시에 대한 hyperplane을 구해보자.
\[y_{1}(w_{1}x_{11} + w_{2}x_{12} + b) = 1\] \[y_{2}(w_{1}x_{21} + w_{2}x_{22} + b) = 1\] \[1 \cdot (2\alpha \cdot 1 + 2\alpha \cdot 1 + b) = 1\] \[(-1) \cdot (2\alpha \cdot (-1) + 2\alpha \cdot (-1) + b) = 1\]이를 통해 α, b를 구할 수 있다.
\[4\alpha + b = 1\] \[4\alpha - b = 1\] \[\alpha = 1/4 \ , \ b = 0\]그리고 앞서 구했던 다음 조건에 식을 대입하자.
\[w_{1} = \alpha_{1} + \alpha_{2}\] \[w_{2} = \alpha_{1} + \alpha_{2}\] \[w_{1}x_{1} + w_{2}x_{2} + b = 0\] \[\frac{1}{2}x_{1} + \frac{1}{2}x_{2} + 0 = 0\]이러면 우리가 구하려 했던 최적의 hyperplane을 얻게 되었다.
\[x_{2} = -x_{1}\]Soft-Margin SVM
데이터를 경계를 나눠서 분류할 수 있다면 좋겠지만, 현실세계 데이터는 정확하게 분류하기 힘들다.
그래서 완벽하기 분리시키는 것이 아닌, 약간의 오류를 허용하는 것이 soft-margin SVM이다.
그리고 그 약간의 오류를 슬랙변수 ξ를 넣어서 제약식을 세롭게 정의한다.
ξ는 크사이라고 읽는데, 이는 데이터가 경계를 얼마나 침범했는지를 나타내는 양의 실수 이다.
① ξ = 0 : 완벽한 분류
② 0 < ξ < 1 : margin 침범 (약한 패널티)
③ ξ > 1 : 오분류 (강한 패널티)
그리고 이를 통해 최적화 문제를 다시 정의할 수 있다.
\(\min_{w,b,\xi} \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{n}\xi_i\)
여기서 C는 우리가 정의하는 얼마나 침범을 허용할 것인가에 대한 변수이다.
결론적으로는 margin을 최대화하면서 벌점인 슬랙변수를 최소화하는 최적화 지점을 찾는 것이 목표가 된다.
Hard-Margin 이랑 같은 방식으로 Lagrange를 KKT조건에 맞게 풀어보자.
새로운 최적화 문제를 Lagrange로 정의하면 다음과 같이 쓸 수 있다.
하드마진과 달리 라그랑즈 상수가 한개 더 늘어난 것을 알 수 있다.
KKT조건으로 빠르게 전개해보자.
정지조건에 맞게 편미분을 해주자.
여기서 하드마진과 달리 슬랙변수에 대한 편미분에서 부등식이 나오는것을 알 수 있다
이유는 μ또한 라그랑즈 상수이기 때문에 0이상이다.
αi + μi = C 여기서 αi - C = −μi 이렇게 쓸 수 있고, -μi <= 0 이를 대입해서
αi - C <= 0 따라서 ai <= C가 된다.
결국 슬랙변수는 미분으로 제거가 되고, α와 C 사이의 관계식으로 표현이 된다.
따라서 최종 식은 다음과 같다.
우리는 C를 조절하면서 어느정도까지 오분류를 허용할지 정할 수 있다.
이렇게 Soft-margin SVM 까지 알아보았다.
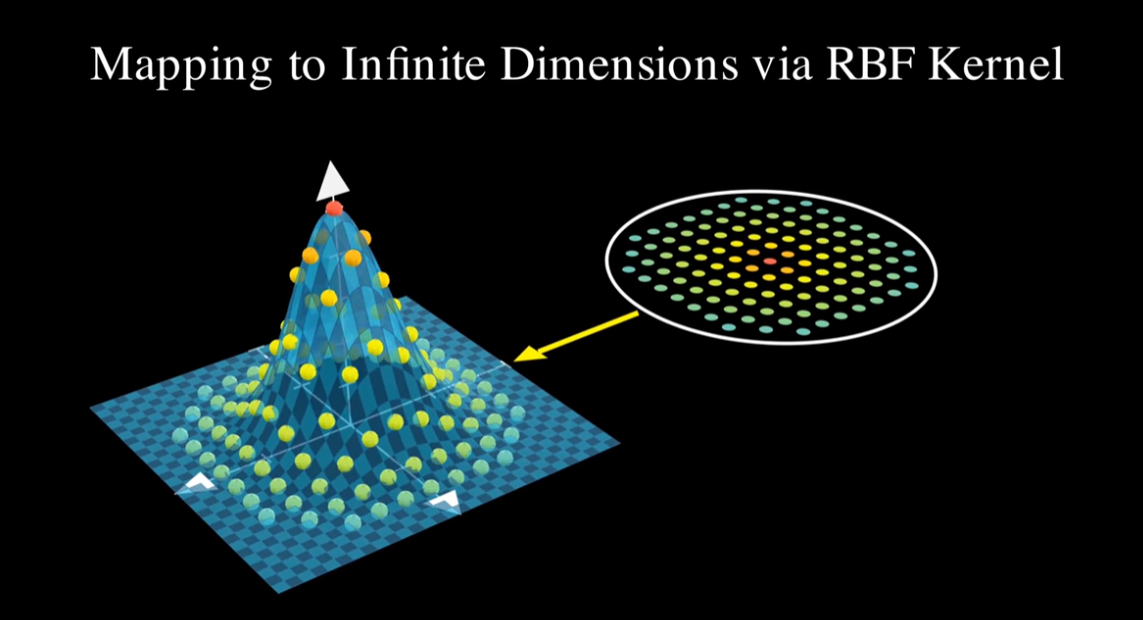
Non-linear SVM
하지만 모든 데이터를 선형으로 분리할 수는 없다.
그럼 다음과 같이 선형 분리가 불가능한 비선형 데이터의 경우에는 어떻게 분리할지 생각해보자.
다음과 같은 데이터일때는 차원을 높여서 문제를 해결 할 수 있다.
그리고 그 경우가 지금 이 포스트의 썸네일이다.

하지만 차원을 높여서 계산을 하면 계산량이 엄청나게 많아진다.
이를 빠르게 계산하기 위해 굳이 차원을 안높이고도 계산할수 있는 방법이 있는데
그것이 Kernel-Trick 이다.
다음은 이 부분에 대해 자세히 알아보도록 하자.
Comments