16 min to read
Comparing Denoising Methods on Time-lapse Image Sequences
연속된 세포 영상이미지에서 노이즈 제거 기법 비교
연속된 세포 영상이미지에서 노이즈 제거 기법 비교
Introduction
바이오 이미징에서 얻어지는 세포 시계열 영상은 실험 환경의 제약 때문에 다양한 형태의 노이즈가 섞여 있다.
조명 강도의 불균일, 센서의 열 잡음, 광독성 때문에 필요한 최소한의 노출 시간만 확보하는 경우 등이 모두 영상 품질 저하의 원인이다.
하지만 연구자가 원하는 것은 세포의 움직임, 분열, 사멸 같은 세부 동역학을 최대한 손실 없이 관찰하는 것이기 때문에, 노이즈 제거는 필수적인 전처리 과정으로 자리 잡아왔다.
노이즈 제거 기법은 크게 통계적 접근법 과 딥러닝 기반 기법 으로 나눌 수 있다.
최근에는 다양한 CNN이나 Transformer 기반 모델들이 좋은 성능을 보이고 있지만,
여전히 전통적인 통계 기반 기법은 빠른 속도, 데이터셋 의존성 없음, 구현 용이성 이라는 장점을 지닌다.
특히 연구 초기 단계나 데이터셋이 제한적인 상황에서는 이러한 기법들이 여전히 유용하다.
대표적인 통계적 노이즈 제거 방법인 Non-Local Means(NLM), BM3D, 그리고 Median Filtering과 Temporal Averaging을 실제 세포 시계열 영상에 적용하고,
실제 노이즈 환경에서의 상대적 비교(SNR proxy)를 통해 각 방법의 특징을 살펴보자.
Data Loading
dataset : Cell Tracking Chellenge
source code : 본문 및 github 참고
우선 사용하는 라이브러리는 다음과 같다
import os, glob
import numpy as np
import cv2
from skimage import img_as_float32
from skimage.metrics import peak_signal_noise_ratio as psnr, structural_similarity as ssim
from skimage.restoration import denoise_nl_means, estimate_sigma
from scipy.ndimage import median_filter, uniform_filter1d
import pandas as pd
import matplotlib.pyplot as plt
import skimage
또한 114개의 frame을 확인하면 너무 오래걸리므로 부분만 확인하는 코드를 짜주자
이때 10 ~ 15 frame을 확인하는 방식을 쓰거나 2칸씩 건너뛰며 전체적인 영상을 살펴보는 방식을 사용할 수 있다
if __name__ == "__main__":
PATH = "test/01"
FILE = "t*.tif"
SCALE = 1.0
START = 10
END = 15
COUNT = None
STEP = 1
OUT_DIR = "results"
os.makedirs(OUT_DIR, exist_ok=True)
def load_files(path, file):
files = sorted(glob.glob(os.path.join(path, file)))
assert len(files) > 0, "path error"
return files
def load_indices(files, idxs, scale = 1.0):
frames = []
for i in idxs:
frame = files[i]
img = cv2.imread(frame, cv2.IMREAD_GRAYSCALE)
if img is None:
raise RuntimeError("fail to read")
if scale != 1.0:
H, W = img.shape
img = cv2.resize(img, (int(W*scale), int(H*scale)), interpolation=cv2.INTER_AREA)
frames.append(img)
# T x H x W matrix
arr = np.stack(frames, 0)
return arr
비교하려는 denoising 기법은 크게 Non-local Means, Median, bm3d, Temporal Averaging 으로 나뉜다.
우선 skimage version에 따라 인자가 바뀌어 오류가 나므로 version에 따라 인자를 맞춰주자
def version(version):
try:
return tuple(int(x) for x in version.split(".")[:2])
except Exception:
return (999,0)
VERSION = version(skimage.__version__) >= (0, 20)
def kwargs():
return {"channel_axis": None} if VERSION else {"multichannel": False}
Median Filter
Median Filter은 한 픽셀 주변값을 정렬한뒤 Median으로 대체하는 denoise 방법이다.
Median을 사용하기 때문에 Mean filter보다 outlier에 robust해 보존력이 높다
# k : 윈도우 크기 (e.g. k=5 -> 5x5 window에서의 median 적용)
def median2d(stack, k=3):
return np.stack([cv2.medianBlur(stack[t], k) for t in range(stack.shape[0])], 0)
def median3d(stack, k=(3,3,3)):
return median_filter(stack, size=k, mode="nearest").astype(stack.dtype)
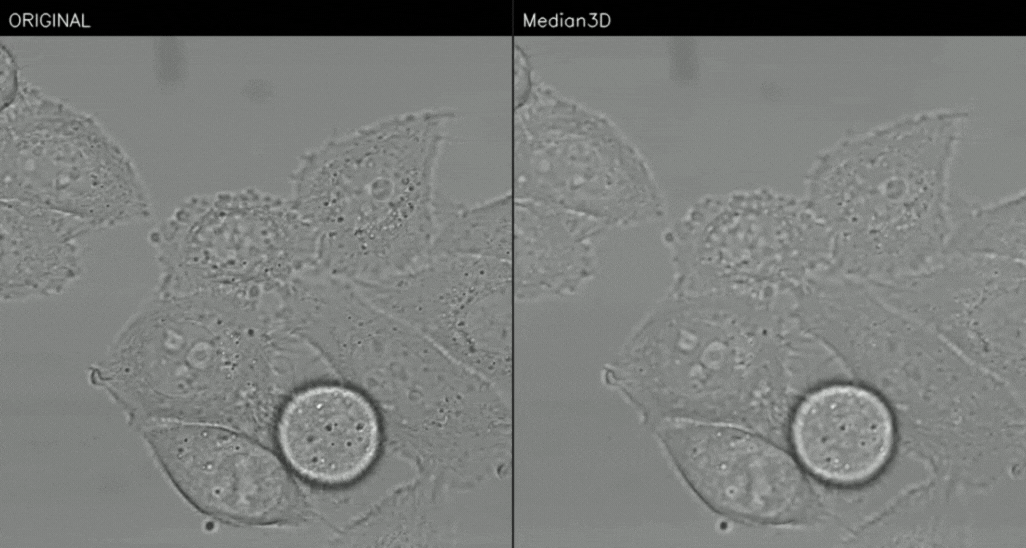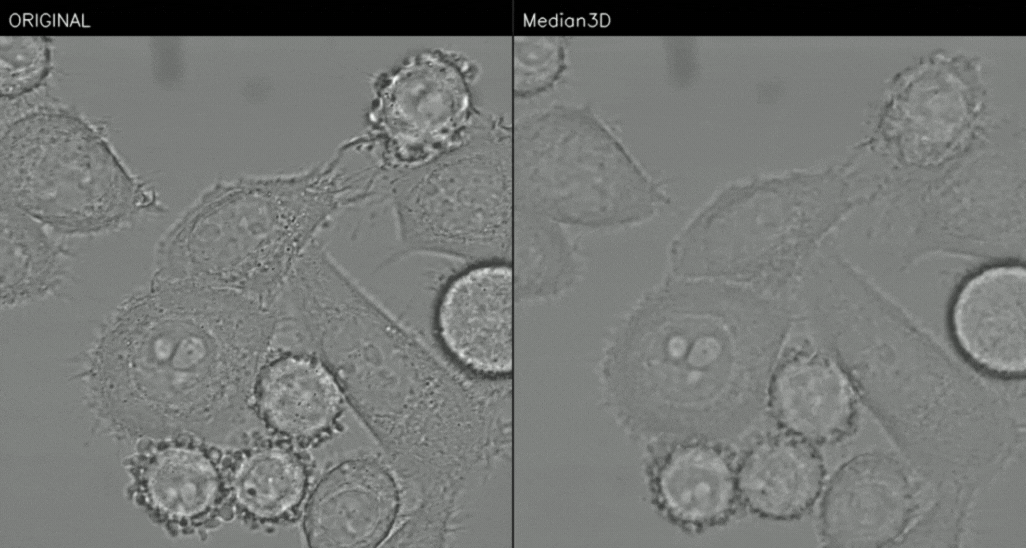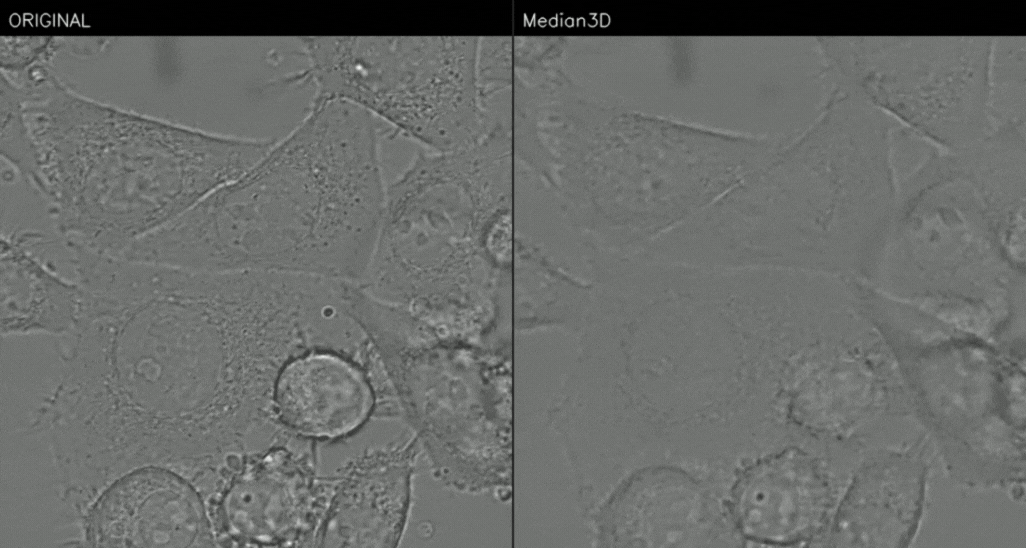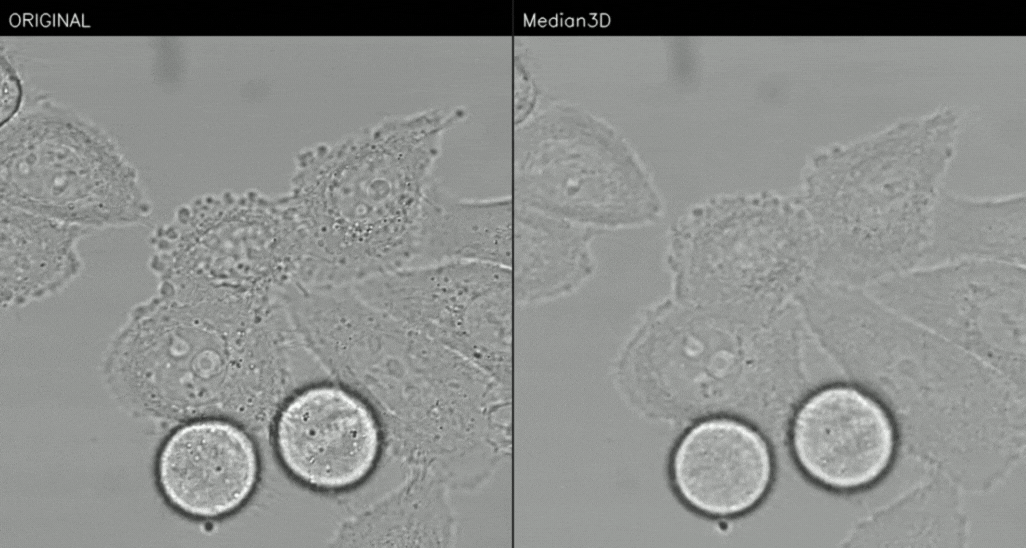
median2d는 현재 이미지 (H x W)에서만 적용하는 거에 비해, median3d는 시간축 (T x H x W) 까지 적용해서 노이즈를 제거한다.
즉, median3d는 현재 이미지 제거하는데 이전과 이후의 이미지도 영향을 준다
노이즈가 랜덤하면 프레임 여러장을 함께보면서 더 강하게 제거할 수 있지만, 움직이는 물체에서는 값이 섞여 blur/ghosting 이 생긴다는 단점도 존재한다.
Non-local Means
먼저 Non-local Means argorithm 이다.
이전 MCD에서의 cell detection에서 사용했던 Gaussian Smoothing 같은 노이즈 제거 알고리즘은 local한 데이터들, 즉 해당 pixel 주변의 정보를 이용한다는데 한계가 존재한다.
이때문에 edge 등이 손실되어 뭉게지는 현상이 발생한다.
Figure 1. Gaussian Smoothing
이에 반해 Non-local Means 는 이름 그대로 local 영역의 pixel이 아닌 해당 pixel 주변 영역과 비슷한 영역을 찾아 평균을 취하는 방식으로 노이즈를 줄이는 기법이다.
즉, 한 pixel 주변 뿐만이 아닌 이미지 전체에서 유사한 구조를 참고하기 때문에 세부 패턴을 더 잘 보존 할 수 있다.
def nlm2d(stack, h):
# skimg 버전별로 인자가 다르기때문에 조정
kwarg = kwargs()
T,H,W = stack.shape
out = np.empty((T,H,W), dtype=np.float32)
for t in range(T):
img = img_as_float32(stack[t])
out[t] = denoise_nl_means(
img,
h=h,
patch_size=5,
patch_distance=3,
fast_mode=True,
**kwarg
)
return np.clip(out*255, 0, 255).astype(np.uint8)
def nlm3d(stack, h):
kwarg = kwargs()
vol = img_as_float32(stack)
try:
out = denoise_nl_means(
vol,
h=h,
patch_size=5,
patch_distance=3
fast_mode=True,
**kwarg
)
except TypeError:
out = denoise_nl_means(
vol,
h=h,
patch_size=5,
patch_distance=3,
**kwarg
)
return np.clip(out*255, 0, 255).astype(np.uint8)
마찬가지로 nlm2d하고 nlm3d차이도 시간축의 유무이다.
코드에서 보이다싶이 2d는 각 이미지들을 고려하는 반면, 3d는 stack을 집어넣어 앞뒤 프레임도 고려하여 필터링하다.
Temporal Average
Temporal Average는 가장 간단한 형태의 시간축 기반 노이즈 제거 방법이다.
def temporal_avg(stack, win=3):
return np.clip(uniform_filter1d(stack.astype(np.float32), size=win, axis=0, mode="nearest"), 0, 255).astype(np.uint8)
코드 또한 시간축(T 방향)으로 윈도우 크기만큼 이동 평균을 수행하는 것을 볼 수 있다.
BM3D (Block-Matching and 3D Filtering)
BM3D는 앞 전 알고리즘에 비해 복잡하지만, 가장 성능이 좋은 노이즈 제거 알고리즘이다.
Block-Matching : 이미지에서 기준 패치와 비슷한 패치를 찾아서 그룹화
3D Stack : 비슷한 2D 패치들을 쌓아 3차원 배열 형성
Collaborative Filtering : 비슷한 패치들을 모아 3차원 stack으로 쌓으면, 3D stack내에서 강한 상관관계를 가지기 때문에, sparse하게 표현할 수 있다
이때 작은 계수들은 thresholding/attenuation으로 제거해서 노이즈를 제거해준다
여기서 sparsity 는 신호나 벡터를 특정 basis로 옮겼을때 중요한 정보는 몇 개 큰 계수에만 몰려있고 나머지는 0에 가까운 것을 의미하다
그리고 이를 다시 역변환 시켜주면 완성이다.
이 방법론은 노이즈 억제력이 좋고, 유사 패치끼리 처리하기때문에 보존력도 좋지만, 계산량이 많다는 단점이 있다.
따라서 차원을 낮춰 2차원으로 적용하자
from bm3d import bm3d, BM3DProfile
def bm3d2d(stack, sigma_psd):
out = []
for t in range(stack.shape[0]):
y = img_as_float32(stack[t])
den = bm3d(y, sigma_psd=sigma_psd, profile=BM3DProfile())
out.append(np.clip(den*255,0,255).astype(np.uint8))
return np.stack(out,0)
SNR
위 방법론을 적용한뒤 평가할 지표를 알아보자
SNR은 Signal to Noise Ratio로 말 그대로 신호와 잡음의 상대적인 크기를 비교하는 것이다.
즉, noise에 비해 신호과 얼마나 명확한지, 잡음에 비해 얼마나 영향을 받는지 정도를 알 수 있다.
def snr_proxy(img):
vals = []
for t in range(img.shape[0]):
thr, _ = cv2.threshold(img[t], 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
bg = img[t][img[t] < thr]
fg = img[t][img[t] >= thr]
if len(bg) < 10 or len(fg) < 10:
continue
vals.append(np.mean(fg) / (np.std(bg)+1e-6))
return float(np.mean(vals)) if vals else np.nan
Otsu는 앞 전 MCD 세포영상에서도 사용했는데, 이는 어떤 이미지나 영상을 thresholding 하고 싶을때, 적정한 threshold값을 찾아주는 알고리즘이다.
이를 사용해 적당한 임계값을 자동으로 찾아 SNR을 계산해서 평가하는 코드이다.
SNR 식은 간단히 설명하면 평균신호 / 배경표준편차 라고 생각하면 쉽다.
Application
이제 방법론을 모두 적용해보자
def run(path, file, scale = 1.0,
START = 0, END = 10, COUNT = None, STEP = 1
):
files = load_files(path, file)
idxs = list(range(START, END + 1, max(1, STEP)))
frames = load_indices(files, idxs, scale)
sig_est = sigma_estimate(img_as_float32(frames[0])) * 255
h2d = 1.0 * sig_est / 255.0
h3d = 1.0 * sig_est / 255.0
methods = []
methods.append(("2D_NLM", nlm2d(frames, h=h2d)))
methods.append(("3D_NLM", nlm3d(frames, h=h3d)))
methods.append(("Median2D_k3", median2d(frames, k=3)))
methods.append(("Median3D_k333",median3d(frames, k=(3,3,3))))
methods.append(("TempAvg_w3", temporal_avg(frames, win=3)))
methods.append(("BM3D", bm3d2d(frames, sigma_psd=20/255.0)))
rows = []
for name, den in methods:
rows.append({"method":name,"SNR_proxy":snr_proxy(den)})
df = pd.DataFrame(rows).sort_values("SNR_proxy", ascending=False)
return df, frames, methods, idxs
Comparing & Visualization
if __name__ == "__main__":
PATH = "test/01"
FILE = "t*.tif"
SCALE = 1.0
START = 10
END = 15
COUNT = None
STEP = 1
OUT_DIR = "results"
os.makedirs(OUT_DIR, exist_ok=True)
print("[1/3] Load & Running")
df, frames, methods, idxs = run(
PATH, FILE, SCALE,
START = START, END = END, COUNT=COUNT, STEP=STEP,
)
print("Complete")
print("[2/3] Metrics")
csv_path = os.path.join(OUT_DIR, f"metrics_t{idxs[0]:03d}_to_t{idxs[-1]:03d}_step{STEP}.csv")
df.to_csv(csv_path, index=False)
print(df)
print("Complete")
top3 = list(df["method"].values[:3])
method_dict = {name: den for (name, den) in methods}
ncols = len(idxs)
BASE_FOR_COMPARE = "GT"
base_vol = frames
for m in top3:
fig, axes = plt.subplots(2, ncols, figsize=(3*ncols, 6))
if ncols == 1:
axes = np.array([[axes[0]], [axes[1]]])
for c in range(ncols):
axes[0, c].imshow(base_vol[c], cmap="gray", vmin=0, vmax=255)
axes[0, c].set_title(f"t={idxs[c]:03d}")
axes[0, c].axis("off")
axes[1, c].imshow(method_dict[m][c], cmap="gray", vmin=0, vmax=255)
axes[1, c].axis("off")
axes[0, 0].set_ylabel("ORIGINAL", rotation=90, fontsize=12)
axes[1, 0].set_ylabel(m, rotation=90, fontsize=12)
plt.tight_layout()
out_png = os.path.join(
OUT_DIR, f"pair_{m}_{BASE_FOR_COMPARE}_t{idxs[0]:03d}_to_t{idxs[-1]:03d}_step{STEP}.png"
)
plt.savefig(out_png, dpi=150)
plt.show()
print("Done.")
Figure 2. SVG_Score
결과를 보면, 여러 노이즈 제거 기법 중 3D Median 필터 가 가장 높은 SNR_proxy(21.9)를 보여 가장 효과적인 방법임을 확인하였다.
단순 시간 평균(TempAvg, win=3) 역시 19.9로 준수한 성능을 나타내어, 시간축에서의 평활화만으로도 상당한 노이즈 억제가 가능함을 보여준다.
반면, 정지 영상에서 강력한 성능을 보이는 BM3D는 본 데이터셋에서는 16.9에 그쳐 기대에 비해 낮은 성능을 보였으며, 이는 움직이는 연속적 이미지셋이기 때문이라고 추정된다.
2D 기반 기법(2D Median, 2D_NLM)과 3D NLM은 상대적으로 낮은 성능을 기록하였으며, 특히 3D NLM은 13.9로 최저치를 보였다.
종합적으로, 본 데이터에서는 복잡한 비정형 패치 기반 알고리즘보다는 단순한 3D 기반 필터링이 안정적이고 효과적인 선택임이 드러났다.
Figure 3. Median_3D
확실히 원본과 비교하면 노이즈가 다수 없어졌지만 조금 흐릿해진 것을 확인할 수 있다.
Comments