5 min to read

Statistical Methods

A survey of Statistical Methods

Featured image

Statistical Methods

Introduction

데이터 분석에서 통계적 기법(statistical methods)은 복잡한 데이터로부터 의미있는 패턴을 찾아내고, 불확실성을 정량화해서, 신뢰할 수 있는 결론을 도출하는게 핵심적인 역할을 한다.

통계적 기법은 추정(estimation)과 가설검정(hypothesis testing)에서부터 회귀(regrassion), 시계열분석, 차원 축소, 군집화 등 광범위하게 사용되고 있다.

Data Exploration

데이터 분석 과정 전에 수행하는 전처리 과정으로 데이터 자체에 대한 주요 특성을 이해하는 과정으로 대표적으로 요약 통계(Summary Statistics)와 데이터 시각화 (Data Visualization)이 있다.

단변량 분석 (Uni-variate Analysis)

특정한 하나의 특징(feature)이 가지고 있는 특성을 파악하는 과정으로 데이터의 중심점, 퍼짐 정도, 범위 등 활용한다.

연속형 변수에 대한 단변량 분석

중심위치에 관련된 척도 (Measure of Central Tendency)

산술평균 (Mean, Arithmetic Mean, AM)

cf. 기하평균 (Geometric Mean, GM), 조화평균(Harmonized Mean, HM)

중앙값 (Median)

주어진 데이터에서 가운데 있는 값

cf. 평균의 함정

최빈값 (Mode)

가장 빈도가 큰 값으로 복수개가 나올 수 있다

변동성 척도 (Measure of Dispersion)

변동성은 데이터들의 퍼짐 정도로 범위가 같다고 변동성이 같은 것은 아니다.

분산 (Variance)

편차 제곱의 평균값으로 다음과 같이 쓴다

\[\sigma^2 = E[(X-E[X])^2]\]

그리고 표준 편차 (Standard Variation) 은 분산의 제곱근인 σ 로 쓴다

변동계수 (Coefficient of Variation, CV)

분산을 평균으로 나눈 값으로 평균으로 나눔으로써, 단위를 맞춰준다

연속형 확률변수의 분포

균등분포 (Uniform Distribution)

지수분포 (Exponential Distribution)

정규분포 (Normal Distribution)

카이제곱분포 (Chi-square Distribution)

다변량 분석 (Multi-variate Analysis)

동시에 2개 이상의 변수들 간의 관계를 파악하는 과정이다

선형관계의 척도

2개 변수가 선형관계의 여부를 파악하는 척도이다

공분산 (Covariance)

\[cov(X,Y) = E[(X-E[X])(Y-E[Y])]\]

공분산 값이 양수일 경우 2개의 변수가 함께 증가하거나 감소함을 의미하고, 음수일 경우는 그 반대이다.

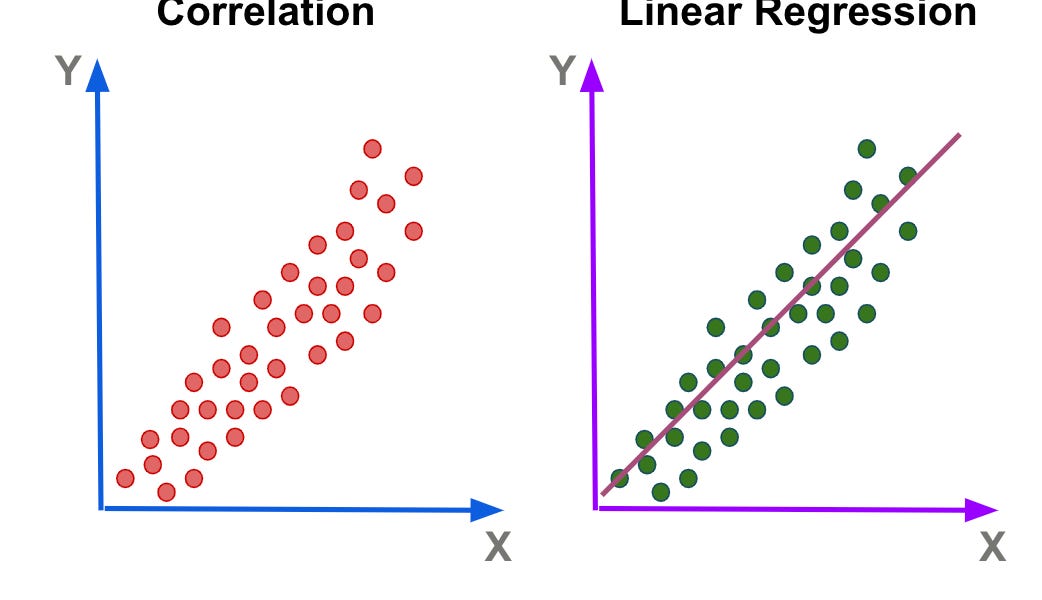
상관계수 (Correlation Coefficient)

공분산을 두 변수의 표준 편차의 곱으로 나눈 값 (비율)으로 상관계수의 절댓값이 0에 가까우면 상관관계가 없음을 의미하고, 1에 가까울수록 상관관계가 강함을 의미한다

상관계수는 인과관계를 제시하지 않으며 어느것이 원인이고 결과인지 알 수 없다

\[\rho_{X,Y} = \frac{cov(X,Y)}{\sigma_X\sigma_Y}\]

유사도 척도 (Silimarity Measure)

두 객체가 얼마나 유사한지의 정도를 실수 값으로 표현한다. Clustering, Classification 등에서 사용되며, 일반적으로 거리 기반 유사도를 많이 사용한다.

단일 속성의 유사도

명목형 (Nominal) 데이터

구분 연산만 가능하며, 거리기준으로 같으면 0, 다르면 1 그리고 유사도는 같으면 1, 다르면 0으로 사용한다.

서수형 (Ordinal) 데이터

순서화가 가능하며, 구분 연산이 가능하다

\[d = \frac{|X-Y|}{n-1}, \ s = 1-d\]

구간형 (Interval) 데이터

구분 연산, 순서 연산 등이 가능하다

\[d = |X-Y|\]

다중 속성의 유사도

Euclidean Distance

가장 많이 쓰는 유사도 척도 중 하나로 두 점 (p,q) 사이의 직선 거리이다.

\[d(p,q) = \sqrt{(p-q)^2}\] \[d(p,q) = \sqrt{(q_1-p_1)^2+(q_2-p_2)^2}\] \[d(p,q)=\sqrt{(p_1-q_1)^2+(p_2-q_2)^2+....+(p_n-q_n)^2}\]

유클리디안 거리의 특징은 제곱한 값의 합이므로 항상 양수이며, p,q간의 거리와 q,p간의 거리는 동일하다.

흔히 아는 피타고라스 공식과 동일하기 때문에 Triangle Inequality가 성립한다.

Cosine Similarity

n차원 공간의 데이터는 vector로 생각할 수 있기 때문에, 유사도 척도로 cosine을 사용할 수 있다. (SVM 같은 classificatiion 모델에서 내적을 결정함수로 사용하는 이유 중 하나이다)

\[a ·b = \|a\|\|b\|cos\theta\] \[similarity = cos\theta = \frac{A·B}{\|A\|\|B\|} = \frac{\sum_{i=1}^{n}A_i\times B_i}{\sqrt{\sum(A_i)^2}\times\sqrt{\sum(B_i)^2}}\]

vector의 크기가 아니라 뱡향의 유사성을 판별한다

1 : 방향 동일 = 거의 유사

0 : 90도 (직교) = 거의 무관

-1 : 180도 반대방향

회귀 분석 (Regression)

변수들 간의 관계를 추정하는 통계적 방법론으로 가장 기본적이지만 매우 광범위하게 사용된다.

주어진 데이터로부터 회귀 모델을 추정한다 (지도학습)

회귀 모델 (Regression Model)

출력에 대한 입력의 평균 효과에 대한 설명 또는 정량화를 위해 사용하며 새로운 값에 대한 결과 값을 에측한다

인과 관계를 위한 설명 모델링과 예측에 대한 예측 모델링으로 나뉜다.

선형 회귀 모델 (Linear Regression Model)

회귀 모형이 직선 형태일때 사용되며 가장 많이 사용된다.

단순 회귀 모델 (독립변수 1개, 2차원)

\[Y=f(X)=\beta_0+\beta_1X+\epsilon_i\]

다중 회귀 모델 (독립변수 2개 이상, 다차원)

\[Y=f(X_1,X_2,....,X_p) = \beta_0+\beta_1X_1+...+\beta_pX_p+\epsilon_i\]

회귀 계수 추정

최소제곱법 (Least Square Method) : 잔차 제곱합이 최소가 되도록 회귀 직선을 계산한다.

경사하강법 (Gradient Descent) : 잔차 제곱합이 적어지는 쪽으로 이동해 최소값에 도달한다

선형 회귀 모델에서의 기본 가정

선형성 : 가장 기본적인 가정으로 종속 변수 Y는 독립변수 X들과 선형결합으로 표현할 수 있어야 한다.

독립성 : 다중 회귀 모델에서만 해당되며, 독립변수간에는 상관관계가 없어야 한다. 다중공선성이 있다면 제거해야한다.

등분산성 : 잔차의 분산은 독립변수 값과 무관하게 일정해야 한다

정규성 : 잔차의 분포는 정규분포에 가까워야한다

비선형 회귀 모델

회귀 모형이 선형이 아닌경우 사용한다

n차 다항 모델 (n-th Order Polynomial Model)

\[y = \beta_0 + \beta_1x + \beta_2x^2 + ... +\beta_nx^n + \epsilon\]

곡선 적합 (Curve Fitting)

훈련 데이터는 모집단 전체가 아니기 때문에 함수 형태를 가정해야 한다

n개 데이터에 대해 (n-1)차 다항 함수를 선택한다면 모두를 지나는 곡선이 가능하지만 다중 공선성에 의한 부작용이 발생할 수 있다

편향-분산 딜레마 (Bias-Variance Dilemma)

일반적으로 높은 차수의 함수를 사용하면 훈련 데이터에 대해 가장 적합한 표현 생성 (노이즈, 부적합한 훈련 데이터까지) 하여 추정된 회귀 함수의 변동성 증가와 새로운 데이터에 대한 예측력이 저하 될 수 있다. -> 과잉적합으로 분산 (variance) 증가

하지만 낮은 차수의 함수를 사용하면 규칙성을 제대로 반영못해 편향이 상승한다

평향 분산을 모두 최소화하는 학습자료는 현실적으로 불가능

로지스틱 회귀 (Logistic Regression)

이진 분류 (binary classification)를 위해 확률을 예측하는 모델이다

종속변수 y는 연속형 데이터가아닌 이산형 (이항분포)데이터가 나와야 하며, 확률로 나와야 하기 때문에 0,1사이 값이 나온다

cf. Poisson Regression

일반적인 선형회귀 식을 사용하면, 연속형 데이터가 나오기 때문에 실수값 Y 범위를 확률값 p 범위 [0, 1]로 모델링하는 Logistic 함수를 사용한다

\[logit = ln(\frac{p}{1-p})=ln(Odds)=\beta_0+\beta_1x_1+...\]

y\sim Bernouㅣㅣ이진 분류 (binary classification)를 위해 확률을 예측하는 모델이다

종속변수 y는 연속형 데이터가아닌 이산형 (이항분포)데이터가 나와야 하며, 확률로 나와야 하기 때문에 0,1사이 값이 나온다

cf. Poisson Regression

일반적인 선형회귀 식을 사용하면, 연속형 데이터가 나오기 때문에 실수값 Y 범위를 확률값 p 범위 [0, 1]로 모델링하는 Logistic 함수를 사용한다

\[logit = ln(\frac{p}{1-p})=ln(Odds)=\beta_0+\beta_1x_1+...\] \[y\sim Bernoulli(p)\]

선형 회귀를 이산적인 이진 분류에 적용할 때 Sigmoid 함수를 사용함으로써 [0,1]로 변환한다.

\[p(xwin) = f(t) = \frac{e^t}{e^t+1} = \frac{1}{1+e^{-t}}\]

선형식 = logit(p), 확률 = sigmoid(linear) 서로 역함수 관계이다